Pekiştirmeli Öğrenme - Bölüm 6: Temporal-Difference (Zamansal Fark) Öğrenmesi
Temporal-Difference (Zamansal Fark) Öğrenmesi
Pekiştirmeli öğrenmenin temel yöntemlerinden biri olan zamansal fark öğrenmesi, daha önceki bölümlerde gördüğümüz dinamik programlama ve Monte Carlo yöntemlerinin bir çeşit kombinasyonudur. Monte Carlo yöntemlerindeki gibi bu yöntemde de ortamın modelini öğrenmeye ihtiyaç duyulmaz. Aynı zamanda dinamik programlamada olduğu gibi en son sonucu beklemeden diğer tahminlerden yardım alarak tahminlerini günceller.
Her zaman olduğu gibi önce bu yöntemin tahmin kısmını (verilen politika için değer fonksiyonunu tahmin etmek), daha sonra ise kontrol (en iyi politikayı bulmak) kısmını inceleyeceğiz. Yukarıda ismi geçen üç yöntemin tahmin kısımları temel olarak benzerdir ve asıl farklılık bunların tahmin kısmına yaklaşımlarındadır.
Zamansal Fark Öğrenmesinde Öngörü Problemi
Monte Carlo yöntemlerinde olduğu gibi zamansal fark öğrenmesinde de öngörü probleminin çözümünde deneyimlerden yararlanılır. Basitçe anlatmak gerekirse ikisinde de politika takip edilir ve alınan sonuca göre tahminler güncellenir. Aralarındaki fark ise Monte Carlo yöntemlerinde tahmini güncellemek için bölüm sonunda elde edilen toplam ödülü \((G)\) beklemeniz gerekirken, zamansal fark öğrenmesinde sadece bir sonraki ödülü kullanarak tahmin güncellenir. Bu farkı daha iyi anlamak için bu yöntemlerin tahmin güncelleme kurallarına bakabilirsiniz.
Monte Carlo tahmin güncelleme kuralı:
\[V(S_t) \leftarrow V(S_t) + \alpha\big[G_t - V(S_t)\big]\]Zamansal Fark Öğrenmesi tahmin güncelleme kuralı:
\[V(S_t) \leftarrow V(S_t) + \alpha\big[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\big]\]Bu iki formül arasındaki fark yakınsama (convergence) için \(V(S_t)\)’nin ulaşması gereken hedeflerdir. \(V(S_t)\) ile ulaşması gereken hedef arasındaki farka da hata denir. Zamansal fark öğrenmesinde sadece bir sonraki adımın ödülü ve değer tahmini kullanılırken, Monte Carlo yöntemlerinde, her bir adım için hesaplanan bu değerlerin azaltılmış toplamı kullanılır. Bu yüzden Monte Carlo kuralındaki hata, zamansal fark öğrenmesindeki hata kullanılarak formülize edilebilir ve şu formül elde edilir:
\[\displaystyle\sum\limits_{k=t}^{T-1}{\gamma^{k-t} \delta_k}\]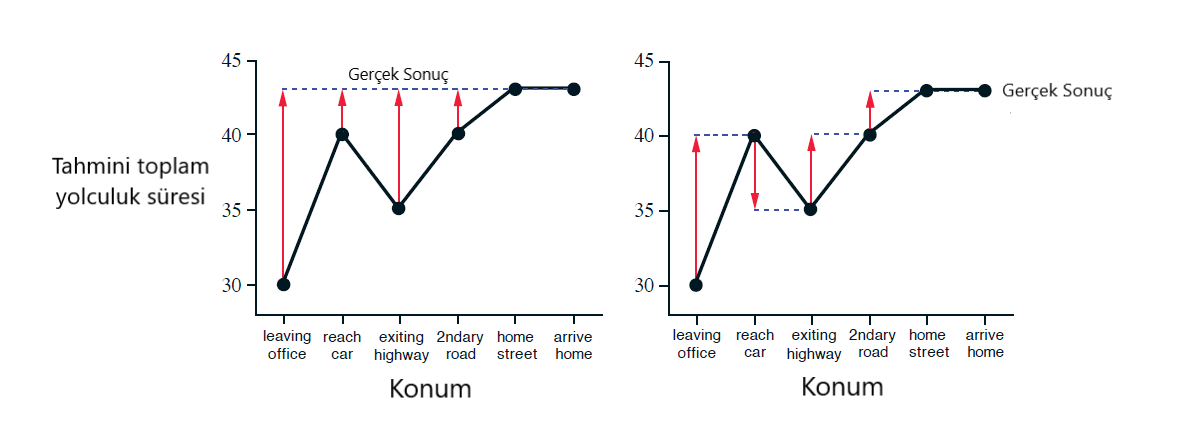
Şekil 6.1 : Eve sürüş örneğinde Monte Carlo yöntemleri (solda) ve TD yöntemleri (sağda) tarafından önerilen değişiklikler.
Tahmin probleminde Zamansal Fark Öğrenmesinin Avantajları
Zamansal fark öğrenmesi, zamansal fark öğrenme açıkça görülebileceği gibi ortamın modeline ihtiyaç duymamaktadır. Bu özelliği dinamik programlamaya göre en önemli avantajıdır.
Monte Carlo yöntemlerine karşı en önemli avantajı ise bölüm sonunu beklemeden tahminlerini güncelleyebilmesidir. Bazı pekiştirmeli öğrenme problemlerinde bölümler çok uzun olabilir ve tahmin güncellemesini yapmak için bölüm sonunu beklemek algoritmayı verimsiz hale getirir. Örneğin gerçek hayatta, bir işin ne zaman biteceğini tahmin etmeye çalışıyorken, tahmininizin gerçekçi olmadığını farkedip hemen yeni bir tahmin yapmanız size büyük avantaj sağlar.Bunun dışında, Monte Carlo yöntemlerinde deney amaçlı eylemlerin alındığı bazı bölümler göz ardı edilmek ya da azaltımlı olarak dikkate alınmak zorundadır ve bu da öğrenmeyi yavaşlatır. Zamansal fark öğrenmesi yöntemlerinde her bir eylem öğrenme için kullanıldığı için böyle bir sorun yaşanmaz.
Zamansal fark öğrenmesi yöntemlerinin, herhangi bir sabit politika için yeteri kadar küçük adım boyu kullanılarak en iyi politikaya yakınsadığı ispatlanmıştır. Ayrıca matematiksel olarak ispatlanmasa da, pratikte zamansal fark öğrenmesi yöntemleri genellikle Monte Carlo yöntemlerinden daha hızlı yakınsar. Örnek 6.2’de basit bir uygulama için bu iki yöntemin yakınsama hızları karşılaştırılmıştır ve zamansal fark öğrenmesi yöntemlerinin istikrarlı bir şekilde daha hızlı yakınsadığı gözlenmiştir.

Örnek 6.2 : Random Walk : Bu örnekte,TD(0)’ın tahmin yeteneklerini ampirik(empirically) olarak karşılaştırdık,sabit- \(\alpha\) yukarıdaki Markov Ödül Sürecine tabi tutultuğunda Monte Carlo.
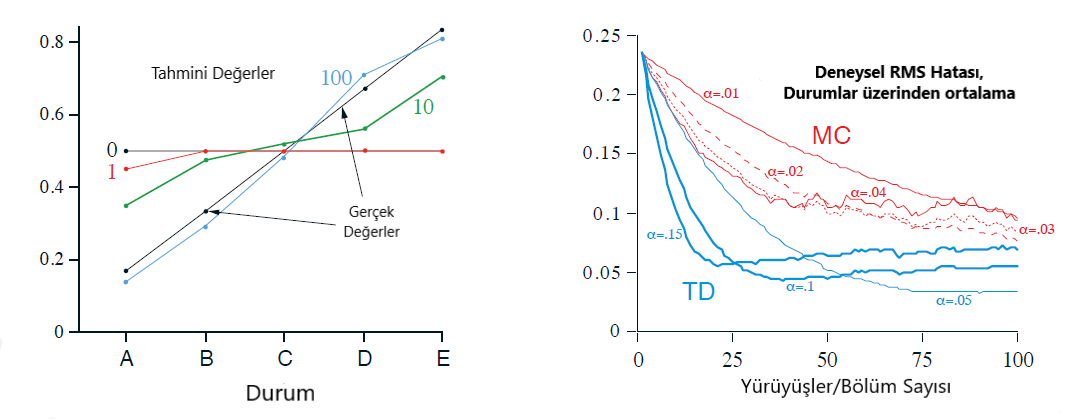
Örnek 6.2 : Random Walk : Yukarıdaki sol grafik, tek bir TD (0) çalışmasında çeşitli sayıda bölümden sonra öğrenilen değerleri göstermektedir. 100 bölümden sonraki tahminler, sabit bir adım boyutu parametresiyle (bu örnekte \(\alpha\) = 0:1) gerçek değerlere geldikleri kadar yakındır, değerler en son bölümlerin sonuçlarına cevaben tamamen nitelendirilir. Sağdaki grafikte ise ikisi için (TD ve MC) öğrenme eğrilerinin farklı \(\alpha\) değerlerinin sonuçlarını gösterir. Gösterilen performans ölçüsü, durumlara göre ortalaması alınan ve daha sonra yüzden fazla çalışmanın ortalamasının alındığı öğrenilen değer fonksiyonu ve gerçek değer fonksiyonu arasındaki bir karekök hatasıdır. Her durumda, yaklaşık değer fonksiyonu tüm \(s\) için ara değer \(V(s)\) = 0:5 olarak başlatıldı. TD yöntemi, bu görevdeki MC yönteminden sürekli olarak daha iyiydi.
Zamansal Fark Öğrenmesinin En Uygunluğu (Optimality)
Eldeki deneyimin yani verinin kısıtlı olduğu durumlarda, en yaygın kullanılan yöntem bu verinin tekrar tekrar kullanıldığı artımlı öğrenmedir (incremental learning). Bu yöntemde tahmin güncellemeleri her adımda hesaplansa da, güncelleme bu güncellemelerin toplamı olarak tek seferde yapılır. Buna toptan güncelleme (batch updating) denir çünkü güncelleme bir deneyim yığınının (batch) tamamını deneyimledikten sonra yapır.
Kısıtlı deneyimle artımlı öğrenme uygulandığında Monte Carlo ve zamansal fark öğrenmesi yöntemleri farklı bir sonuca yakınsar. Bunun nedenini anlamak için bir örneği inceleyelim. Elimizde aşağıda görebileceğiniz 8 bölümlük deneyim var.
\begin{align}
A,0,B,0 & \ \ B,1
B,1 \ \ \ & \ \ B,1
B,1 \ \ \ & \ \ B,1
B,1 \ \ \ & \ \ B,0
\end{align}
Bu deneyimleri incelediğimizde, ilk bölümde A’dan başlanıp B’de sona ulaşılmış ve hiç ödül alınmamış. Diğer bölümler daha kısa ve hepsinde B’de başlanıp direkt sona ulaşılmış. Bu örnekte A ve B durumlarının değerlerini tahmin etmemiz gerekiyor. B’nin değerinin \(6/8\) olduğunu herkes kolayca görebilir sanırım. Peki A durumunun değeri ne olmalı? Burada iki farklı yaklaşım söz konusu. Birincisinde B durumunda yaptığımız gibi gördüğümüz tüm A’lar 0 dönüş sağladığı için A’nın değeri 0 diyebiliriz. Diğerinde ise sistemi bir Markov süreci gibi modelleyerek, A her zaman B’ye gidiyor ve B’nin değeri \(3/4\) olduğu için A’nın da değeri \(3/4\) olmalı diyebiliriz. Monte Carlo kullanıldığında birinci sonuç \((V(A)=0)\) elde edilirken, zamansal fark öğrenmesi yöntemleriyle ikinci sonuç \((V(A)=3/4)\) elde edilir. Elimizdeki kısıtlı veri için Monte Carlo metodunun sonucu daha doğruyken, test verisinde zamansal fark öğrenmesinin yaklaşımının daha doğru olması beklenir.
Bu örnekten anlaşılacağı gibi Monte Carlo yöntemleri her zaman eldeki veri için hatayı en aza indirmeye çalışırken, zamansal fark öğrenmesinde ise en olası markov süreci için gerçek değer tahmin edilir. Zamansal fark öğrenmesinde tahmin edilen markov süreci doğruysa tahmin edilen değer kesin olarak doğrudur bu yüzden ona kesinlik denkliği (certainty equivalence) tahmini denir. Bu aynı zamanda, zamansal fark öğrenmesi yönteminin daha hızlı yakınsamasını sağlar.
Zamansal Fark Öğrenmesiyle Politikalı (On-policy) Kontrol
Şimdiye kadar zamansal fark öğrenmesinin tahmin problemini görmüştük. Şimdiyse kontrol problemine geçiyoruz. Normalde olduğu gibi genelleştirilmiş politika iterasyonunu(GPI) uyguluyoruz ama bu sefer değerlendirme veya tahmin için zamansal fark öğrenmesi yöntemlerini kullanıyoruz.
İlk adım durum değer fonksiyonu yerine aksiyon değer fonksiyonu öğrenmektir. Politikalı yöntemlerde \(q_{\pi}(s,a)\) fonksiyonu o anki politika ve her durum, eylem çifti için tahmin etmek gerekiyor. Bunu temel olarak yukarıda \(v_{\pi}\) fonksiyonu için yaptığımız şekilde yapabiliriz. Sarsa için tahmin güncelleme kuralı:
\begin{align} Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha\big[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)\big] \end{align}
Bu güncelleme her bir eylemden sonra yapılır ve eğer \(S_{t+1}\) bir uç(terminal) durum ise \(Q(S_{t+1},A_{t+1})\) sıfır alınır. Sarsa tahmin metoduna dayanan kontrol algoritmasında \(q_{\pi}\) sürekli olarak tahmin edilir ve aynı zamanda politika \(\pi\) daha açgözlü(greedy) olacak şekilde güncellenir.
Q-Öğrenmesi: Zamansal Fark Öğrenmesiyle Politikasız (Off-policy) Kontrol
Bu yöntemde Sarsa’dan farklı olarak öğrenilen eylem-değer fonksiyonu bir politikadan bağımsız olarak en iyi eylem-değer fonksiyonuna yakınsar. Politika hala etkindir ama onun tek amacı tüm durum-eylem çiftlerinin güncellenmeye devam ettiğinden olmaktır. Q-Öğrenmesi için tahmin güncelleme kuralı:
\begin{align} Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha\big[R_{t+1} + \gamma \max\limits_a Q(S_{t+1},a) - Q(S_t,A_t)\big] \end{align}
Bu formülde görebileceğiniz gibi Sarsa metodunda politika tarafından seçilen \(A_{t+1}\), Q-Öğrenmesi metodunda tabloya bakılarak en yüksek değeri veren eylem olarak seçilir.
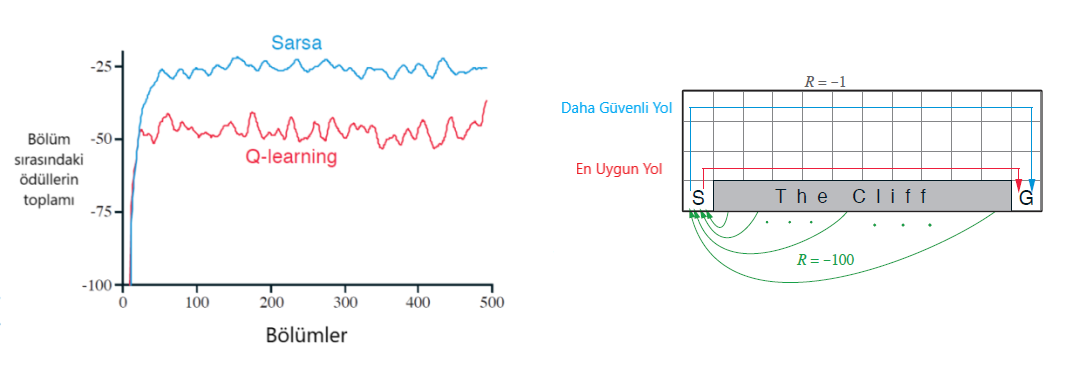
Örnek 6.6 : Cliff Walking : Sarsa ve Q-öğrenmesi karşılaştırılması,politika içi (Sarsa) ve politika dışı (Q-learning) yöntemleri arasındaki fark.
Beklentili (Expected) Sarsa
Beklentili Sarsa metodu \(Q\)-öğrenmesine çok benzer ama bu yöntemde \(A_{t+1}\) olarak en yüksek değeri veren eylemi almak yerine olası eylemlerin beklenen değeri(expected value) kullanılır. Beklenen değer, olası eylemlerin politikaya göre seçilme ihtimali ile onların \(Q\) tablosundaki değerlerinin çarpımının toplamı şeklinde hesaplanır. Bu değişikliği yaptığımızda tahmin güncelleme kuralı şu hale gelir:
\begin{align} Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha\big[R_{t+1} + \gamma \mathbb{E}[Q(S_{t+1},A_{t+1})\mid S_{t+1}] - Q(S_t,A_t)\big] \end{align}
veya beklenen değer formülünü açarak şu şekilde gösterilebilir:
\begin{align} Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha\big[R_{t+1} + \gamma \sum\limits_a{\pi(a\mid S_{t+1})Q(S_{t+1},a)} - Q(S_t,A_t)\big] \end{align}
Bu yöntem aynı zamanda Sarsa’ya da çok benzer çünkü ikisinde de \(A_{t+1}\) politika tarafından seçiliyor. Sarsa metodunda güncelleme yapılırken de seçilen \(A_{t+1}\) kullanılırken, Beklentili Sarsa’da o durumun beklenen değeri kullanıldığı için bu yöntem böyle adlandırılmıştır. Beklentili Sarsa aynı zamanda politikasız olarak da kullanılabilir. Örneğin \(A_{t+1}\) seçiminde açgözlü bir politikalı kullanılıp hedef politika olarak (\(A_t\) seçiminde) \(\epsilon\)-açgözlü bir politika kullanırsa Beklentili Sarsa metodu \(Q\)-Öğrenmesine dönüşür.
Beklentili Sarsa metodu Sarsa’ya göre hesaplama açısından daha karmaşıktır ama \(A_{t+1}\)’in rastgele seçilmesinden kaynaklanan değişintiyi ortadan kaldırdığı için genelde daha iyi performans gösterir.
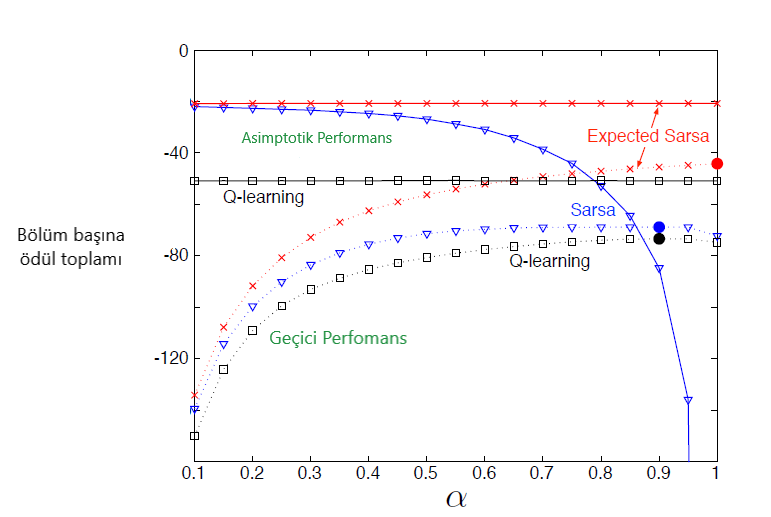
Şekil 6.3 : \(\alpha\) ‘nın bir fonksiyonu olarak cliff-walking görevi üzerinde TD kontrol yöntemlerinin geçici ve asimptotik performansı. Tüm algoritmalar “\(\epsilon\)-açgözlü(greedy)” politikası kullanmakta olup \(\epsilon\) = 0:1. Asimptotik performans ortalama 100.000 bölümden fazlayken, ara performans ilk 100 bölümün ortalamasıdır.Bu veriler, geçici ve asemptomatik vakalar için sırasıyla 50.000 ve 10 çalışmanın ortalamalarıdır. Kesintisiz daireler her yöntemin en iyi ara performansını gösterir. van Seijen ve arkadaşları tarafından uyarlanmıştır. (2009)
Enbüyütme (Maximization) Sorunu ve İkili Öğrenme (Double Learning)
Şimdiye kadar bahsettiğimiz tüm yöntemler algoritmalarında enbüyütme(maximization) işlemine sahiptir. Örneğin, \(Q\) öğrenmesinde tahmin güncellemesinde \(A_{t+1}\) olarak en yüksek değere sahip eylemi seçiyoruz. Sarsa ve diğer yöntemlerde de genelde \(\epsilon\)-açgözlü(greedy) politikalar kullanıldığı için onlarda da enbüyütme yapılır. Bu enbüyütme işlemi, algoritmalarda en büyütme sorununa yol açar yani algoritmada iyimser bir yaklaşıma, pozitif önyargıya sebep olur.
Enbüyütme işleminin neden sorun olduğunu anlamak için bir örnek verelim. Bütün olası eylemlerin sıfır değere sahip olduğu bir durumdayız. Ama algoritma bu değerlerden emin olmadığı için ortalaması yaklaşık sıfır olan tahminler yapar yani bazı tahminler pozitiftir. Bu durumda algoritma yanılır ve orada artı değerli bir eylem varmış gibi davranır.
Enbüyütme sorununun en önemli sebeplerinden biri hem en büyük değeri bulurken hem de onun değerini tahmin ederken aynı ajanın kullanılmasıdır. Bunu çözmek için iki farklı ajanın kullanıldığı ikili öğrenme tekniği kullanılır. İkili öğrenme tekniğini yukarıdaki tüm zamansal fark öğrenmesi yöntemlerine uygulayabiliriz. Örneğin \(Q\) öğrenmesine uyguladığımızda tahmin güncelleme kuralı şu hale gelir:
\begin{align}
Q_1(S_t,A_t) \leftarrow Q_1(S_t,A_t) + \alpha\big[R_{t+1} + \gamma Q_2(S_{t+1},arg_a maxQ_1(S_{t+1},a)) - Q_1(S_t,A_t)\big]
\end{align}
Bölümlerin yarısında yukarıdaki \(Q_1\) güncellenirken diğer yarısında formüldeki \(Q_1\) ve \(Q_2\)’ler yer değiştirir ve \(Q_2\) güncellenir.
Oyunlar, Durum Sonrası (Afterstates) ve Diğer Özel Durumlar
Kitaptaki algoritmaların genel yaklaşımı eylem değer fonksiyonu öğrenmek üzerine olsa da bazı durumlarda istisnalar olabiliyor. Örneğin birinci bölümdeki XOX oyununda durum değer fonksiyonuna daha çok benzeyen bir fonksiyon öğrenilmeye çalışılmıştı. Ama bu oyunda normalden farklı olarak hamle yapıldıktan sonraki pozisyonların değeri tahmin ediliyordu. Bu hamle sonrası pozisyonlara durum sonrası diyebiliriz.
Durum sonrası değer fonksiyonu öğrenmek satranç, tic-tac-toe gibi ortamın bazı dinamiklerini bildiğimiz durumlarda faydalıdır. Örneğin tic-tac-toe oyununda, iki farklı durum-eylem çifti bize aynı pozisyonu verebilir ve bunların değerlerinin tek tek hesaplanması yerine direkt durum sonrası pozisyonun değerinin hesaplanması öğrenmeyi hızlandırır.
Tüm özel durumları tek tek anlatmak imkansız ama bu kitapta anlatılan temel prensipler çoğu problem için uygulanabilir. Örneğin durum sonrası değer fonksiyonu öğrenmek özel bir durum olsa da yine yukarıda anlatılan yöntemlerle benzer bir algoritmaya sahiptir.
Özet
Bu bölümde zamansal fark öğrenmesi yöntemlerini ve onların pekiştirmeli öğrenme problemlerinde nasıl kullanıldığını gördük. Zamansal fark öğrenmesinin Monte Carlo ve dinamik programlama yöntemleriyle ilişkisini ve onlara göre avantajlarını inceledik.
Daha sonra en temel ve sık kullanılan zamansal fark öğrenmesi yöntemleri olan Sarsa, \(Q\)-öğrenmesi ve beklentili Sarsa yöntemlerini ve onların farklarını inceledik. Sarsa politikalı bir yöntemdir ve tüm eylemleri bu politika tarafından belirlenir. \(Q\)-öğrenmesi ise politikasızdır ve güncelleme kuralında politika tarafından seçilen \(A_{t+1}\) yerine olası eylemlerden en büyük değeri olan kullanılır. Beklentili Sarsa methodu ise politikalı veya politikasız olabilir. Bu yöntemde ise \(A_{t+1}\)’in değeri olarak olası eylemlerin beklenen değeri alınır.
Bu yöntemlerin dışında zamansal fark öğrenmesinin ileriki bölümlerde göreceğimiz farklı versiyonları da vardır. Bunlar n adımlı zamansal fark öğrenmesi ve aktör-kritik yöntemleridir.
