Pekiştirmeli Öğrenme - Bölüm 7: n-Adım Paketleme
n-Adım Paketleme
\(n\)-adım yöntemi, ara algoritmaların iyi performans gösterdiği şekilde, Monte Carlo yöntemleri ile tek-adım zamansal fark yöntemlerini birleştirdiği için pekiştirmeli öğrenmede önemli bir yaklaşımdır. \(n\)-adımlı yöntemler, bir ucunda Monte Carlo metotları ve diğerinde tek\(-\)adım zamansal fark yöntemleri olan bir spektruma sahiptir. \(n\)-adım yöntemleri, öğrenimi zaman adımı (time step) zorunluluğundan kurtardığı için avantajlı olmaktadır.
n-Adım TD Tahmini
Monte Carlo yöntemleri, her durum için, bölümün sonuna kadar gözlemlenen ödüllerin sırasına göre bir güncelleme gerçekleştirir. Diğer yandan, tek adım zamansal fark metodunun güncellemesi, geri kalan ödüller için bir vekil olarak bir sonraki aşamada durumun değerinden paketleme yapılmasına dayanmaktadır. Bir çeşit ara metot, daha sonra, bir ara tutara dayanan bir güncelleme gerçekleştirecektir: adım adım artar. Örneğin, iki aşamalı bir güncelleme ilk iki ödül ve iki adım sonra durumun tahmini değerine dayanacaktır. Aşağıdaki şekilde soldaki tek adım zamansal fark güncellemesi ve sağdaki sonlandırmaya kadar Monte Carlo güncellemesi ile \(v_{\pi}\) için \(n-\)adım güncellemelerinin spektrumunun yedek diyagramlarını göstermektedir.
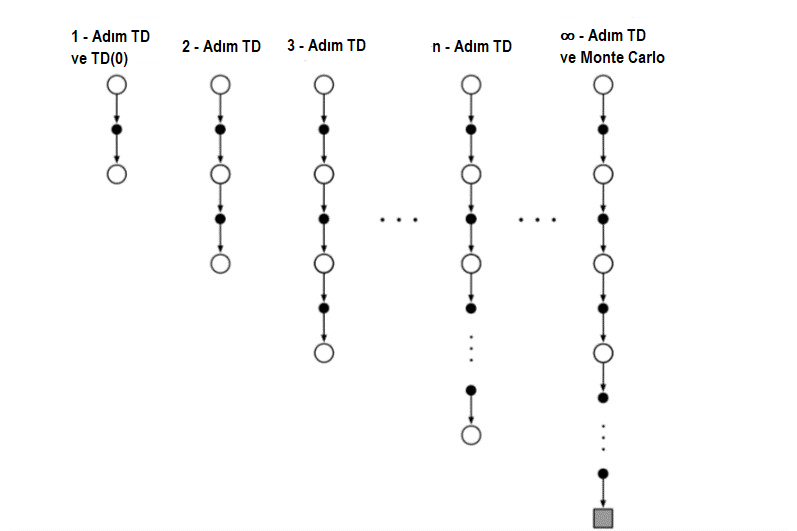
Şekil 7.1 : n-adım yöntemlerinin yedek diyagramları. Bu yöntemler bir adım TD yöntemlerinden Monte Carlo yöntemlerine kadar değişen bir spektrum oluşturur.
\(n-\)adım güncellemelerini kullanan metotlar hala TD(Temporal Difference) metotlarıdır, çünkü daha sonraki bir tahminin nasıl farklı olduğuna bağlı olarak daha önceki bir tahmininin değişmesine neden olurlar. Şimdi bir sonraki tahmin bir adım değil, \(n-\)adım sonra. TD’nin \(n-\)adımlı işlemlerine \(n-\)adım TD metodu denir.
Durum-ödül dizisi (eylemlerin ihmal edilmesi) sonucu olarak, \(S_{t}\) durumunun tahmini değerinin güncellenmesini dikkate alır. Monte Carlo’da güncellemenin \(v_{\pi}(S_{t})\) tahmininin tam dönüş yönünde güncellendiğini biliyoruz:
\begin{align} G_{t}\doteq R_{t+1}+\gamma R_{t+2} +\gamma^{2} R_{t+3}+…+\gamma^{T-t-1} R_{T} \end{align}
Monte Carlo güncellemelerinde hedef, dönüştür, tek\(-\)adım güncellemeler de hedef, ilk ödül ve bir sonraki durumun indirgenmiş tahmini değeridir.
\begin{align} G_{t:t+1}\doteq R_{t+1}+\gamma V_{t}(S_{t+1}) \end{align}
Şimdiki amacımız, bu fikrin, bir adım sonrasında yaptığı gibi, iki adım sonrasında da mantıklı hale gelmesi. İki adımlı güncellemenin hedefi iki adımlı geri dönüş:
\begin{align} G_{t:t+2}\doteq R_{t+1} +\gamma R_{t+2} + \gamma^{2}V_{t+1}(S_{t+2}) \end{align}
Burada \(\gamma^{2}V_{t+1}(S_{t+2})\) formülü \(\gamma R_{t+2} +\gamma^{2} R_{t+3}+...+\gamma^{T-t-1} R_{T}\) terimlerin yokluğu için düzeltme işlemi yapar. Benzer şekilde, \(n-\)adım bir güncelleştirme için hedef \(n-\)adım geri dönüşlüdür: \begin{align} G_{t:t+n}\doteq R_{t+1} +\gamma R_{t+2} + … +\gamma^{n-1}R_{t+n}+ \gamma^{n}V_{t+n-1}(S_{t+n}) , \qquad (7.1) \end{align}
Tüm \(n-\)adımlı dönüşler, tam dönüş için yaklaşık olarak kabul edilebilir, n adımdan sonra kesilir ve sonra kalan eksik terimler için \(V_{t+n-1}(S_{t+n})\) ile düzeltilir. Eğer \(t+n \geq T\) (eğer \(n-\)adım geri dönüşü sona erer ya da öteye uzanırsa), o zaman bütün eksik terimler sıfır olarak alınır ve \(n-\)adımlı dönüş, normal tam dönüşe eşit olarak tanımlanır (\(t+n \geq T\) ise \(G_{t:t+n}\doteq G_{t}\)).
n-adımlı dönüşleri kullanmak için doğal durum-değer öğrenme algoritması , \begin{align} V_{t+n}(S_{t})\doteq V_{t+n-1}(S_{t})+\alpha [G_{t:t+n-1} - V_{t+n-1}(S_{t})] , \quad 0 \leq t < T \qquad (7.2) \end{align}
Diğer tüm durumların değerleri değişmeden kalır: \(V_{t+n}(s)=V_{t+n-1}(s)\) için \(s \neq S\) . Biz bu algoritmaya \(n-\)adımlı zamansal fark diyoruz. Her bölümün ilk \(n-1\) adımları sırasında hiçbir değişiklik yapılmadığını unutmayın. Bunu telafi etmek için, bölümün sonunda, sonlandırmadan sonra ve bir sonraki bölüme başlamadan önce eşit sayıda ek güncelleme yapılır.
\(n-\)adımlı dönüşünün önemli bir özelliği, beklentilerinin, \(V_{t+n-1}\)‘nin daha kötü bir anlamda, daha iyi bir \(v_{\pi}\) tahmini olması garantilidir. Yani, beklenen \(n-\)adımlı dönüşün en kötü hatası, \(V_{t+n-1}\) altındaki en kötü hatanın \(\gamma^{n}\) değerinden küçük veya ona eşit olacak şekilde garanti edilir:
\[\max_{s}\mid E_{\pi} \left[G_{t:t+n} \mid S_{t} =s \right] -v _{t}(s) \mid \leq \gamma ^{n} \max_{s} \mid V_{t+n-1}(s)-v_{\pi}(s)\mid , \qquad (7.3)\]tüm \(n\geq 1\) için. Buna \(n\) adımlı geri dönüşlerin hata azaltma özelliği diyoruz. Hata indirgeme özelliğinden ötürü, tüm \(n-\)adım zamansal fark metotlarının uygun teknik koşullar altında doğru tahminlere yakınlaştığı resmen gösterilebilir. \(n-\)adım zamansal fark metotları, tek adım zamansal fark metotları ve kesin üyeler olarak Monte Carlo metodu ile bir sağlam/güvenilir metotlar ailesi oluşturur.
\(n-\)Adım Sarsa
\(n-\)adım metodu, sadece tahmin problemleri için değil kontrol işlemleri içinde kullanılmaktadır. Bu kısımda, \(n-\)adım metotlarının, doğru bir şekilde TD yöntemine yönelik bir kontrol yöntemi üretme yolunda Sarsa ile nasıl birleştirilebileceğini anlatılmakta. Sarsa’nın \(n-\)adım versiyonunu “\(n-\)Adım Sarsa” olarak adlandırıp bir önceki bölümde sunduğumuz orijinal versiyonuna bundan sonra “tek adım Sarsa” veya “Sarsa(0)” olarak adlandırırız.
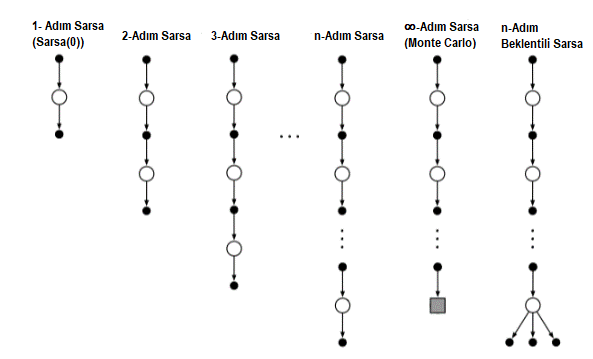
Şekil 7.3 : Durum-eylem değerleri için \(n\)-adım yöntemlerinin spektrum yedek diyagramları. Bunlar, Sarsa(0)’ın bir adım güncellemesinden Monte Carlo yönteminin sonlandırma güncellemesine kadar uzanmaktadır. Bunlar arasında, \(n\)-adım güncellemeleri, gerçek ödüllerin \(n\)-adımlarına ve sonraki tüm durum-eylem çiftinin tahmini değerine bağlı olarak güncellenir. En sağdaki Beklenen \(n\)-adım Sarsa için diyagram.
Ana fikir, yalnızca durumları, eylemler (durum-eylem çiftleri) için değiştirmek ve daha sonra bir \(\epsilon -\)açgözlü davranış politikası kullanmaktır. \(n-\)adım Sarsa için yedek diyagram (Şekil 7.2)’de gösterilen) \(n-\)adımlı TD metodunda (Şekil 7.1) olduğu gibi Sarsa hepsinin bir durum yerine bir eylemle başlayıp bitmesi dışında, alternatif durumlar ve eylemler dizileridir.
Tahmini işlem değerleri açısından \(n-\)adım dönüşleri (güncelleme hedefleri) yeniden tanımlarız:
\begin{align} G_{t:t+n} \doteq R_{t+1}+\gamma R_{t+2}+…+ \gamma^{n-1} R_{t+n} + \gamma^{n} Q_{t+n-1} (S_{t+n}, A_{t+n}) ,n\geq 1, 0\leq t < T-n \qquad (7.4) \end{align}
O zaman algoritmanın doğal hali aşağıdaki gibidir.
\begin{equation} \label{eq:75} Q_{t+n}(S_{t},A_{t})\doteq Q_{t+n-1}(S_{t},A_{t})+\alpha [G_{t:t+n} - Q_{t+n-1}(S_{t},A_{t})], 0 \leq t < T \qquad (7.5) \end{equation}
Geri kalan durumların değerleri değişmeden kalırsa: tüm \(s\) ve \(a\) için \(Q_{t+n}(s,a)=Q_{t+n-1}(s,a)\), \(s\neq S, a\neq A\). Bu, bahsedilen \(n-\)adımlı Sarsa algoritmasıdır. Tek adım yöntemlerine kıyasla öğrenmeyi hızlandırabilmesinin bir örneği Şekil 7.4’te verilmiştir.
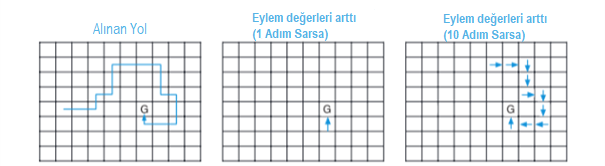
Şekil 7.4 : Gridworld, n-adım yöntemlerinin kullanımı nedeniyle davranış politikası öğreniminin hızlandırılması örneğidir. İlk panel, bir agent tarafından tek bir bölümde alınan ve G tarafından işaretlenen yüksek bir ödülle sonuçlanan yolu gösterir. Bu örnekte, değerler başlangıçta 0’dı ve tüm ödüller, G’de olumlu bir ödül dışında sıfırdı. Diğer iki paneldeki oklar, tek adım ve n-adım Sarsa yöntemleriyle bu yolun sonucu olarak hangi eylem değerlerinin güçlendirildiğini gösterir. Tek adım metodu, yüksek ödüle yol açan eylem dizisinin yalnızca son eylemini güçlendirirken, \(n\)-adımlı metot, dizinin son \(n\) eylemlerini güçlendirir, böylece bir bölümden çok daha fazlası öğrenilir.
Sarsa’nın \(n-\)adımlı dönüşünün, yeni bir zamansal fark hatası ile tam olarak yazılabildiğini kanıtlamak istenirse,
\begin{align} G_{t:t+n} = Q_{t-1}(S_{t},A_{t})+\displaystyle \sum\limits_{k = t}^{\min(t+n,T)-1} \gamma ^{k-t}[R_{k+1}+\gamma Q_{k}(S_{k+1},A_{k+1})- Q_{k-1}(S_{k},A_{k})] \qquad (7.6) \end{align}
Beklenen Sarsa’nın (Expected Sarsa) \(n-\)adım için yedek diyagramı, Şekil 7.3 ‘te en sağda gösterilmiştir. \(N-\)adım Sarsa’da olduğu gibi, lineer bir dizi örnek eylem ve durumdan oluşur, ancak son unsuru, her zaman olduğu gibi, \(\pi\) altındaki olasılıklar ile ağırlıklandırılmış tüm eylem olasılıkları üzerinde bir daldır. Bu algoritma, \(n-\)Adım Sarsa ile aynı denklemle tanımlanabilir.
\[\label{eq:77} G_{t:t+n}\doteq R_{t+1} +...+\gamma^{n-1}R_{t+n}+ \gamma^{n}\overline{V}_{t+n-1}(S_{t+n}), t+n<T \qquad (7.7)\]\(\overline{V}_{t}(s)\) ‘nin, hedef davranış politikasının altında, \(t\) zamanında tahmin edilen eylem değerlerini kullanarak, durumun beklenen yaklaşık değeri olduğu durumlar:
\(\label{eq:78} \overline{V}_{t}(s)\doteq \sum_{a}\pi (a|s) Q_{t}(s,a), \qquad (7.8)\) tüm \(s\) \(\in S\) için
Beklenen yaklaşık değerler, bu kitabın geri kalanında birçok işlem değeri yönteminin geliştirilmesinde kullanılır. \(s\) uç ise, beklenen tahmini değer \(0\) olarak tanımlanır.
\(n-\)Adım Politika dışı (Off-Policy) Öğrenme
Hatırlayacak olursak politika dışı öğrenme, bir davranış politikası için değer fonksiyonu \(\pi\)’yi, başka bir politika takip ederken \(b\)’yi öğrenmekte. Genellikle \(\pi,\) mevcut eylem-değer-fonksiyon tahmini için aç gözlü yaklaşım ve \(b\) ise \(\epsilon\)-açgözlü daha açıklayıcı bir keşif politikasıdır. Verileri \(b\)‘den kullanabilmek için, iki politika arasındaki farkı dikkate alarak, alınan eylemleri alma olasılığını kullanmak zorundayız (bkz. Bölüm 5.5). \(n-\)adım metotlarda, geri dönüşler \(n\) adımın üzerine inşa edilir, bu yüzden sadece \(n\) eylemlerinin nispi olasılığı ile ilgileniyoruz.
Örneğin, \(n-\)adım TD yönteminin basit bir davranış politikasız versiyonunu yapmak için, \(t\) (sadece \(t + n\) zamanında yapılan) zaman güncellemesi, \(p_{t:t+n-1}\) tarafından basitçe ağırlıklandırılabilir.
\begin{equation} \label{eq:79} V_{t+n}(S_{t})\doteq V_{t+n-1}(S_{t})+\alpha p_{t:t+n-1}[G_{t:t+n-1} - V_{t+n-1}(S_{t})] ,0\leq t< T \qquad (7.9) \end{equation}
\(p_{t:t+n-1}\) : Önem örnekleme oranı.
\begin{align} \rho_{t:h} \ \dot{=} \displaystyle\prod\limits_{k=t}^{min(h,T-1)}\dfrac{\pi(A_k|S_k)}{b(A_k|S_k)} \qquad (7.10) \end{align}
Mesela eylemlerden herhangi biri hiçbir zaman \(\pi\) (yani, \(\pi (A_k \mid S_k) = 0\) tarafından tercih edilmezse, \(n\) adım dönüş sıfır ağırlık verilmeli ve tamamen yok sayılmalıdır. Diğer taraftan, eğer tesadüfen, \(\pi\), \(b'\)den çok daha büyük olasılıkla alacağı bir eylem yapılırsa, dönüşe verilecek ağırlığı arttıracaktır. Bu mantıklıdır çünkü bu eylem, \(\pi\) karakteristiğidir, fakat sadece nadiren \(b\) ile seçilir ve bu nedenle nadiren verilerde görülür. Bunu telafi etmek için, meydana geldiğinde ağırlığı arttırmalıyız. İki politika aslında aynıysa (politikadaki durum), örnekleme oranının her zaman \(1\) olduğunu unutmayın. Böylece yeni güncellememiz (7.9), daha önceki \(n\)-adım TD güncellememizi genelleştirip tamamen değiştirebilir. Benzer şekilde, önceki \(n-\)adım Sarsa güncellememiz tamamen basit bir davranış politikasız formla değiştirilebilir:
\begin{equation}
\label{eq:711}
Q_{t+n}(S_{t},A_{t})\doteq Q_{t+n-1}(S_{t},A_{t})+\alpha \rho_{t+1:t+n} [G_{t:t+n} - Q_{t+n-1}(S_{t},A_{t})] , 0 ≤ t < T \qquad (7.11)
\end{equation}
Buradaki örnekleme oranının öneminin, n-adım zamansal farkdan (7.9) bir adım sonra başladığını ve bittiğini unutmayın. Bunun nedeni, burada bir durum eylem çiftini güncelliyoruz. Eylemi seçmemizin ne kadar muhtemel olduğunu umursamıyoruz; bu aşamada, seçtiğimiz eylemin sonraki eylemler için önem örneklemesini bilmek istiyoruz.
Beklenen \(n-\)adım Sarsa’nın davranış politikasız versiyonu, \(n-\)adım Sarsa ile aynı güncellemeyi kullanacaktır, fakat formül (7.11) ‘de görüldüğü gibi denklem \(\rho_{t+1:t+n-1}\) yerine \(\rho_{t+1:t+n}\) kullanır. Beklenen Sarsa’da mümkün olan tüm eylemler son durumda dikkate alınır.
Kontrol Değişkenine göre Karar Verme Metodu (*Per-decision Methods with Control Variates)
Önceki bölümde sunulan çok adımlı politika dışı yöntemler, basit ve kavramsal olarak açıktır, ancak muhtemelen en verimli olan değildir. Daha sofistike bir yaklaşım, Bölüm 5.9 ‘da verildiği gibi, karar başına verilen önem örneklemesi fikirlerini kullanacaktır. Bu yaklaşımı anlamak için, öncelikle, tüm dönüşler gibi sıradan \(n-\)adım dönüşün (7.1) öz yinelemeli olarak yazılabilir. \(h\) horizon’a \(n\) adımda biten, \(n-\)adım dönüşü şöyle yazılabilir,
\[\begin{align*} G_{t:h}=R_{t+1}+ \gamma G_{t+1:h} \qquad (7.12) \end{align*}\]Şimdi, hedef politika \(\pi\) ile aynı olmayan bir davranış politikasını takip etmenin etkisini düşünün. Birinci ödül \(R_{t+1}\) ve bir sonraki durum \(S_{t+1}\) dahil olmak üzere ortaya çıkan deneyimin tümü, \(t\) zaman için, \(\rho_t=\dfrac{\pi(A_t\mid S_t)}{b(A_t\mid S_t)}\) için örnekleme oranının önemine göre ağırlıklandırılmalıdır. Yukarıdaki denklemin sağ tarafına ağırlık vermek için cazip gelebilir, ancak daha iyisini yapabilir. Eylemin \(t\) zamanında asla \(\pi\) ile seçilmeyeceğini, böylece \(p_{t}= 0\) olduğunu düşünelim. Daha sonra basit bir ağırlık, \(n-\)adım dönüşün sıfır olmasıyla sonuçlanacak, bu da hedef olarak kullanıldığında yüksek bir varyansa neden olabilir. Bunun yerine, bu daha sofistike yaklaşımda, \(h\) horizon’a \(n-\)adım dönüş alternatif, politika dışı tanımını kullanır,
\begin{equation} \label{eq:7.13} G_{t:h} \dot{=} \rho_{t}(R_{t+1} + \gamma G_{t+1:h})+(1-\rho_t) V_{h-1}(S_t), \qquad t<h<T \qquad (7.13) \end{equation}
Bu yaklaşımda, \(\rho_{t}\) sıfır ise, hedefin sıfır olması ve tahminin daraltılması yerine, hedef tahmin ile aynıdır ve hiçbir değişikliğe yol açmaz. Örnekleme oranının sıfır olması, örneklemeyi görmezden gelmemiz gerektiği anlamına gelir, bu nedenle tahminin değiştirilmemesi uygun görünmektedir. Kontrol varyasyonunun beklenen güncellemeyi değiştirmediğine dikkat edin; Önem örnekleme oranının bir değer beklemesi (Bölüm 5.9) ve tahmin ile ilişkisiz olması nedeniyle, kontrol değişkeninin beklenen değeri sıfırdır.
Eylem değerleri için, \(n\) adım dönüşün davranış politikasız tanımı biraz farklıdır çünkü ilk eylem, örneklemenin öneminde bir rol oynamaz. İlk eylem, öğrenilen şeydir; Hedef politika kapsamında olası veya imkansız olup olmadığı önemli değil, onu takip eden ödül ve duruma tam birim ağırlık verilmesi gerekiyor. Önem örneklemesi sadece onu takip eden eylemler için geçerli olacaktır.
Öncelikle, eylem değerleri için \(h\) horizonda şeklinde biten \(n-\)adım dönüş beklentisi, beklenti formunun (7, 7), (7.12) ‘de olduğu gibi özyinelemeli olarak yazılabilir. Kontrol değişkenleri ile bir politika dışı biçimi,
\[\begin{align} \label{eq:7.14} G_{t:h} & \dot{=} R_{t+1} + \gamma\bigg(\rho_{t+1}G_{t+1:h} + \overline{V_{h-1}}(S_{t+1}) - \rho_{t+1}Q_{h-1}(S_{t+1}, A_{t+1})\bigg) \qquad (7.14) \\ &=R_{t+1} + \gamma\rho{t+1}\bigg(G_{t+1:h} - Q_{h-1}(S_{t+1},A_{t+1})+\gamma\overline{V_{h-1}}(S_{t+1})\bigg),t < h \leq T \end{align}\]Eğer \(h < T\) ise, o zaman \(G_{h:h}\doteq Q_{h-1}(S_{h},A_{h})\) ile özyineleme biter, buna karşılık eğer \(h \ge T\) ise, \(G_{T-1:h}\doteq R_{T}\) ile öz yineleme biter. Ortaya çıkan tahmin algoritması (sonrasında formül 7.5, ile birleştirilirse) Beklenen Sarsa’ya benzer.
Politika dışı eğitimin davranış politikalı eğitimden daha yavaş olması muhtemelen kaçınılmazdır; sonuçta, veriler öğrenilen şeyle daha az ilgilidir. Ancak, muhtemelen bu yöntemlerin geliştirilebileceği de doğrudur. Kontrol değişkenleri, varyansı azaltmanın bir yoludur.
Önem Örneklemesiz Politika Dışı Öğrenme: n-adım Ağaç Yedekleme Algoritması (Off-policy Learning Without Importance Sampling: The n-step Tree Backup Algorithm)
Bu bölümde, Önem örneklemesi olmadan politika dışı öğrenme için ağaç yedekleme algoritması (tree-backup algorithm) olarak adlandırılan \(n-\)adım yöntemi üzerine durulmuştur.
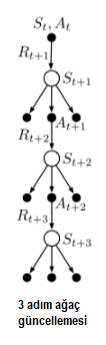
Algoritma fikri, 3-adım ağaç-yedekleme güncellemesi için sağdaki görselde ki gibidir. Ağaç üzerinde \(S_{t}, A_{t}\) durum-eylem çiftinden sonra meydana gelen olayları temsil eden 3 örnek durum ve ödül ve iki örnek eylemden oluşa rastgele değişkenler vardır. Ağacın yaprakları, hiç seçilmeyen eylemleri temsil etmekte. Merkezi omurgayı temsil eden eylemler seçilen iki örnek eylemi temsil eder. 3-adım ağaç yedekleme algoritması için güncelleme ağacın yapraklarından (seçilmeyen eylemlerden) gelir. Seçilmemiş eylemlerin örnek verisi olmadığı için güncelleme oluştururken değerlerini tahmin ederiz. Yani beklenen değerlerini alırız. Bu nedenle ağaç yedekleme güncellemesi (tree-backup update) denir. Gerçek eylemlere karşılık gelen iç mekandaki eylem düğümleri katılmaz. Her yaprak düğüm bir politika altında oluşma olasılığı ve değerinin çarpımı ile toplanarak bulunur. Diyagramda ki bir eylem düğümüne her bir ok, eylemin hedef politika altında seçilme olasılığı ile ağırlıklandırılır ve eylemin altında bir ağaç varsa, bu ağırlık ağacın tüm yaprak düğümlerine uygulanır.
3 aşamalı ağaç yedekleme güncellemesini 6 yarı adımdan oluşan bir süreç olarak düşünebiliriz. Bu, bir eylemden sonraki bir aşamaya kadarki yarım aşamalı adımlar arasındadır. Politika kapsamında gerçekleşmektedir. Şimdi \(n-\)adımlı ağaç yedekleme algoritması için detaylı denklemleri geliştirelim.
Tek adımlı dönüş (hedef), Beklenen Sarsa ile aynıdır,
\begin{equation} \label{eq:7.15} G_{t:t+1} \dot{=} R_{t+1} + \gamma \displaystyle \sum_a \pi(a \mid S_{t+1})Q_t(S_{t+1},a) \qquad (7.15) \end{equation}
Ağaç yedekleme \(n\)-adımlı dönüş ise aşağıdaki gibidir. \begin{equation} \label{eq:7.16} G_{t:t+n} \dot{=} R_{t+1} + \gamma \displaystyle \sum_{a \neq A_{t+1}} \pi(a \mid S_{t+1})Q_{t+n-1}(S_{t+1},a) + \gamma \pi (A_{t+1} \mid S_{t+1}) G_{t+1:t+n} \qquad (7.16) \end{equation}
*Birleştirici Algoritma: \(n\)-adım \(Q\) (\(\sigma\)) Unifying Algorithm: \(n\)-step \(Q\)(\(\sigma\))
Bu bölüme kadar \(n\)-adım Sarsa, \(n\)-adım Ağaç Yedeklemesi(Tree backup) ve \(n\)-adım Beklenen Sarsa algoritmalarını gördük.
- \(n\)-step Sarsa, tüm örnek geçişlere sahiptir.
- Ağaç yedekleme algoritması, örnekleme olmadan tamamen dallanmış tüm harekete geçirici geçişlere sahiptir.
- \(n\)-adım Beklenen Sarsa, son durumdan eyleme geçişi hariç tüm örnek geçişlere sahiptir. beklenen bir değer ile tamamen dallanmış.
Bu bölümde daha önce görmüş olduğumuz algoritmaları Şekil 7.5’in 4. yedekleme şeması ile ifade edilen şekilde birleştirme önerilmiştir. Bu, karar vericinin eylemi Sarsa’daki gibi bir örnek olarak almak isteyip istemediğine ya da ağaç yedekleme güncellemesinde olduğu gibi tüm eylemler üzerindeki beklentiyi dikkate almasının adım adım bazında karar verebileceği düşüncesidir. Daha sonra, eğer her zaman örneklemeyi seçtiyse, kişi Sarsa’yı elde edecekti, oysa hiç biri örneklemeyi seçmezse, ağaç-yedekleme algoritmasını alacaktı. Şekildeki son diyagramın önerdiği gibi, başka birçok olasılık da olacaktır.
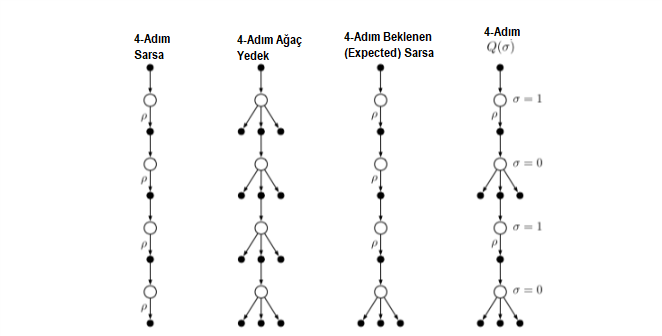
Şekil 7.5 : Bu bölümde (4 aşamalı durum) şimdiye kadar ele alınan üç adımlı n adımlı eylem değeri güncellemelerinin yedek diyagramları ve bunların tümünü birleştiren dördüncü bir güncelleme türünün yedek diyagramı. ‘Ρ’lar, politika dışı vakada önemlilik örneklemenin gerekli olduğu yarı geçişleri belirtir. Dördüncü güncelleme türü, örneklemenin \(\sigma_{t}=1\) olup olmadığına \(\sigma_{t}=0\) göre durum bazında seçim yaparak diğerlerini birleştirir. \(\sigma_{t} \epsilon [0,1]\)
Olanakları daha da artırmak için örnekleme ve beklenti arasında sürekli bir varyasyonu düşünebiliriz. Rastgele değişken \(\sigma_{t}\), \(t\) zamanında durum, eylem veya durum eylem çiftinin bir fonksiyonu olarak ayarlanabilir. Bu önerilen yeni algoritma \(n-\)adım \(Q(\sigma)\) diyoruz.
Önce ağaç-yedekleme \(n\)-adım geri dönüşünü (7.16) \(h = t + n\) cinsinden ve sonra beklenen yaklaşık değer \(\bar{V}\) (7.8) cinsinden yazıyoruz.
\[\begin{align*} G_{t:h} &= R_{t+1}+\gamma\displaystyle \sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q_{h-1}(S_{t+1},a) +\gamma\pi(A_{t+1}|S_{t+1})G_{t+1:h} \\ &=R_{t+1}+ \gamma \bar{V}_{h-1}(S_{t+1})-\gamma \pi(A_{t+1}|S_{t+1})Q_{h-1}(S_{t+1},A_{t+1})+ \gamma\pi (A_{t+1}|S_{t+1})G_{t+1:h} \\ &=R_{t+1}+\gamma \pi(A_{t+1}|S_{t+1}) \bigg(G_{t+1:h} - Q_{h-1} (S_{t+1},A_{t+1}) \bigg)+ \gamma\bar{V}_{h-1}(S_{t+1}), \end{align*}\] \[\begin{align*} G_{t:h} \dot= R_{t+1} &+\gamma \bigg(\sigma_{t+1} \rho_{t+1}+(1- \sigma_{t+1} \pi (A_{t+1}|S_{t+1}) \bigg) \bigg(G_{t+1:h}- Q_{h-1}(S_{t+1},A_{t+1}) \bigg) \\ &+\gamma \bar{V}_{h-1}(S_{t+1}), \qquad \qquad(7.17)\end{align*}\]
Özet
Bu bölümde, bir önceki bölümün bir adım TD yöntemleri ile daha önceki bölümün Monte Carlo yöntemleri arasında yer alan bir dizi zamansal fark öğrenme yöntemi geliştirdik. Orta miktarda bir paketleme gerektiren yöntemler önemlidir, çünkü bunlar genellikle aşırıdan daha iyi performans gösterecektir.
Bu bölümdeki odağımız, bir sonraki \(n\) ödüllere, durumlara ve eylemlere dikkat eden \(n-\)adımlı yöntemler üzerinde olmuştur. Şekil 7.5’te bulunan 4 adımlı yedekleme diyagramı, sunulan yöntemlerin çoğunu birlikte özetler. Gösterilen durum-değer güncellemesi, \(n-\)adımlı TD için önem örneklemesidir ve aksiyon-değer güncellemesi, Beklenen Sarsa ve \(Q\)-öğrenmeyi genelleştiren \(n-\)adım \(Q(\sigma)\) içindir. Tüm n-adımlı metotlar, güncellemeden önce \(n\) zaman adımlarının bir gecikmesini içerdiğinden, sadece o zaman bilinen tüm gelecekteki olaylar olacaktır. Diğer bir dezavantaj, önceki adımlara göre zaman adımında daha fazla hesaplama içermeleridir. Tek adımlı yöntemlerle karşılaştırıldığında, \(n\) adımlı yöntemler, son \(n\) zaman adımları boyunca durumları, eylemleri, ödülleri ve bazen diğer değişkenleri kaydetmek için daha fazla bellek gerektirir. Sonunda, Bölüm 12’de, çok adımlı TD yöntemlerinin, uygunluk izlerini kullanarak minimal bellek ve hesaplama karmaşıklığı ile nasıl uygulanabileceğini göreceğiz, ancak tek adım yöntemlerin ötesinde her zaman ek bir hesaplama yapılacaktır. Bu tür maliyetler, tek bir zaman basamağının zorbalığından kaçmak için bedel ödeyebilir. Her ne kadar \(n-\)adım yöntemleri uygunluk izleri kullananlardan daha karmaşık olsa da, kavramsal olarak açık olmanın büyük yararına sahiptirler. \(n-\)adımında davranış politikasız öğrenmeye iki yaklaşım geliştirerek bundan yararlanmaya çalıştık. Bir önem örneklemesine dayanarak kavramsal olarak basit ama yüksek varyans olabilir. Hedef ve davranış politikaları çok farklıysa, verimli ve pratik olabilmeleri için muhtemelen yeni algoritmik fikirlere ihtiyaç duyar. Diğer, ağaç yedekleme güncellemelerine dayanan, stokastik hedef politikaları olan çok adımlı duruma \(Q\)-öğrenmenin doğal uzantısıdır. Örneklemenin önemi yoktur, ancak yine de hedef ve davranış politikaları büyük ölçüde farklıysa, paketleme işlemi \(n\) büyük olsa bile sadece birkaç adım olabilir.
