Pekiştirmeli Öğrenme - Bölüm 5: Monte Carlo Yöntemleri
Monte Carlo Tahminlemesi
Bir durumun değerinin, o durumdan başlayarak gelecekten beklenen indirgenmiş toplam ödül olduğunu hatırlarsak, söz konusu durumun değerini tahmin etmek için o durumdan sonra gözlemlenen ziyaretlerin dönüş değerlerinin ortalaması alınabilir. Daha fazla sayıda gözlem yapıldıkça ortalama değer beklenen değere yaklaşır. Bu görüş Monte Carlo metodunun temelidir. Bir \(s\) durumunu baz alarak, \(s\)’nin her bir döngüdeki ziyaret edilme durumuna göre iki Monte Carlo metodu vardır: ilk ziyaret (first-visit) ve her ziyaret (every-visit) . İlk Ziyaret’de \(s\)’nin döngüdeki ilk ziyaretinden sonraki dönüşlerin ortalaması alınır. Her Ziyaret metodunda ise \(s\)’nin her ziyaretlerinden sonraki dönüşlerin ortalaması alınır.
Dinamik Programlama(DP) metodu sonraki olayların olasılık dağılımlarına ihtiyacı olduğu için uygulaması kolay değildir. DP için öncelikle tüm ihtimallerin hesaplanması gerekmektedir. DP her bir bölümdeki tüm ihtimalleri hesaplıyorken Monte Carlo’da sadece ilgili durum ve durumlar için sonuç üretebilir. Monte Carlo’da her bir durumdaki tahminler birbirinden bağımsızdır, DP’de olduğu gibi diğer durumları baz almaz. Bu sayede herhangi bir durumun veya seçilen alt durumların tahminlemesi için tüm durumların hesaplanması gerekmez.
Örnek 5.1 : Blackjack : Blackjack’in popüler casino kart oyununun amacı 21’i geçmeden sayısal değerleri mümkün olduğu kadar büyük olan kartları elde etmektir.Tüm yüz olan kartlar 10, as ise 1 veya 11 olarak sayılabilir. Her oyuncunun dağıtıcıya karşı bağımsız olarak rekabet ettiği sürümü düşünüyoruz.Oyun hem dağıtıcıya hem de oyuncuya verilen iki kartla başlar. Krupiyenin kartlarından biri yukarı dönük, diğeri aşağı dönük.
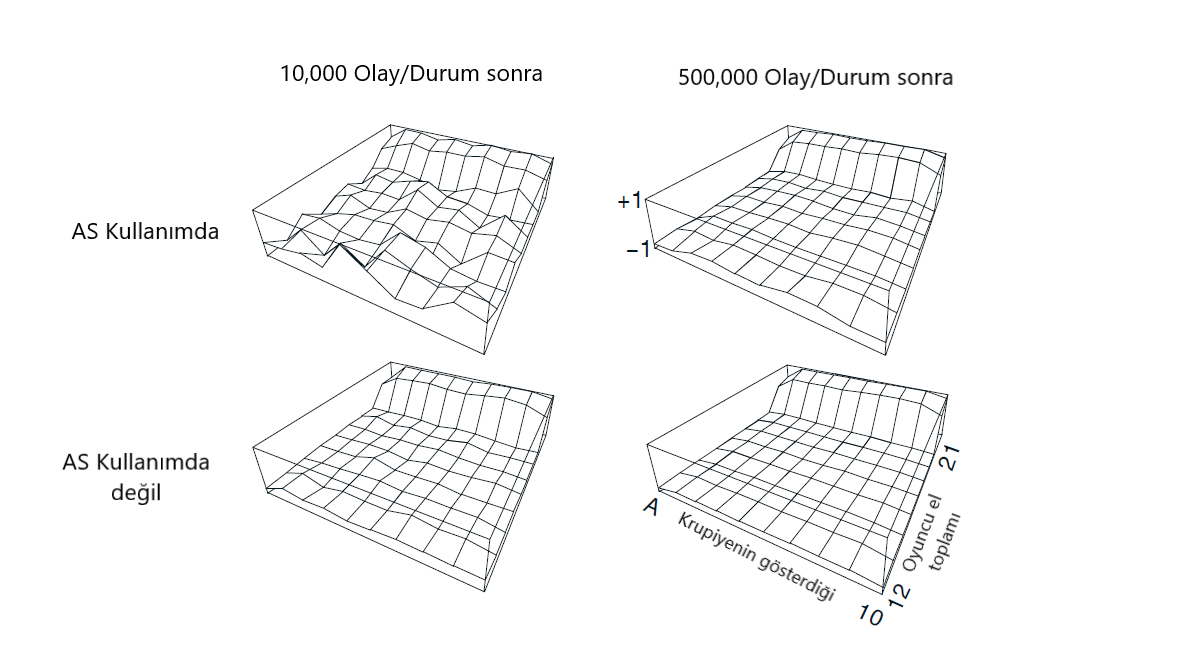
Şekil 5.1 : Approximate state-value functions for the blackjack policy that sticks only on 20 or 21, computed by Monte Carlo policy evaluation.
Eylem Değerlerinin Monte Carlo Tahmini
Herhangi bir model bulunmadığı zaman eylem değerlerini tahmin etmek, durum değerlerini tahmin etmekten daha işlevseldir. Çünkü ortada bir model olmadığında, durum değerleri hangi eylemin gerçekleştirileceği bilgisini tek başına sağlayamaz. Bu yüzden eylem değerleri için politika değerlendirmesi yapılması, politika önerisi yapılırken çok önemlidir.
Eylem değerleri için politika değerlendirmesinde amaç \(q_\pi(s, a)\)’yi yani beklenen getiriyi tahmin etmektir. Monte Carlo metodları bu amacı gerçekleştirirken durum-eylem çiftlerini gezer. Every-Visit Monte Carlo metodu, bir durum-eylem çiftinin değerini tüm ziyaretlerin getirilerinin ortalaması olarak tahmin ederken First-Visit Monte Carlo metodu ise durumun ziyaret edilip eylemin seçildiği ilk getirilerin ortalaması olarak tahmin eder.
Monte Carlo metodlarının tek problemi ise birçok durum-eylem çiftinin gezilmemesidir. Bu nedenle eğer \(\pi\) deterministik ise herhangi bir durum için sadece bir tane eylemin değeri elde edilir. Ortalama bir değer elde edilemediği için de diğer eylemlerin Monte Carlo tahminleri tecrübeyle gelişmez.
Politika değerlendirmesinin birden fazla eylem değeri için çalışması için devamlı olarak keşif yapıldığından emin olunması gerekmektedir. Bunun yollarından birisi tüm durum-eylem çiftlerinin başlangıç olasılıklarının sıfırdan farklı olarak başlatılmasıdır. Buna exploring starts denir.
Exploring starts kullanışlı olsa da özellikle öğrenmenin çevreyle direkt olarak etkileşime girilerek yapıldığı problemlerde güvenilir değildir. Bu tür problemlerde alternatif olarak, tüm durumlara ait eylemlerin herhangi birinin seçilme ihtimali sıfır olmayan stokastik politikalar seçilebilir.
Monte Carlo Kontrolü
Bu bölümde en uygun politikaya yaklaşım yapabilmek için Monte Carlo tahminlerinin kullanılabileceğini göreceğiz. Genelleştirilmiş Politika İterasyonu’nda (GPI) hem politika hem de değer fonksiyonu bulunur ve iyileştirilmeye çalışılır. Sonsuz bölüm deneyimleyeceğimizi ve keşif başlangıçlarının olabileceğini varsayarsak, Politika Değerlendirme ve İyileştirme yöntemleri kullanılarak, \(\pi_k\) için doğru bir \(q_{\pi_k}\) hesaplanabilecektir.
\[\begin{align} \pi(s) \doteq \underset{a}{\operatorname{argmax}} q(s,a). \qquad (5.1) \end{align}\]\(\qquad \qquad \qquad \qquad\) 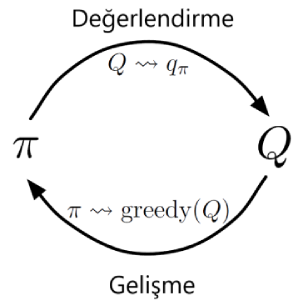
\(\qquad \qquad \qquad \qquad\) Şekil 5.1.1 :Evalution - Improvement

Politika iyileştirmesi, politikayı elimizdeki değer fonksiyonunu kullanarak, daha açgözlü hale getirmeye, politikanın en yüksek değerli eylemi seçmesini sağlamaktır. Bu şekilde Monte Carlo yöntemleri en uygun politikayı bulabilirler.
Keşif başlangıçları ve sonsuz bölüm varsayımlarını sırayla bir kenara bırakalım. Sonsuz sayıda bölüm olmaması durumunda, her politika değerlendirmesinde doğru \(q_{\pi_k}\) hesabına yaklaşıldığı düşünülmelidir. Fakat ne olursa olsun, çok sayıda bölüme ihtiyaç duyulacağı kesindir. Bu yöntemle beraber, belli bir sayıda bölüm deneyimleyerek yaklaşık bir \(q_{\pi_k}\) elde etmeden, politika değerlendirmeye girmemek de bir yöntem olabilir.
Monte Carlo politika değerlendirmesinde bölüm bölüm ilerlemek olağandır. Rastgele bir durum ve eylemden başlayarak bir bölüm sonunda getiriler ile değer fonksiyonu güncellenir, değer fonksiyonu da kullanılarak politika iyileştirilir. Değer fonksiyonu ilgili politika için ideal değer fonksiyonuna yaklaşacağı için politikayı değiştirecek ve nihayetinde en uygun politika ve değer fonksiyonu bulunacaktır.
Keşfi Başlatmadan Monte Carlo Kontrolü
Bu bölümde; genellikle tahmini maksimum eylem değerine sahip olanı seçtikleri için açgözlü (ε-greedy) yöntem olarak kullanılacaktır. Yani, tüm aç gözlü olmayan (non-greedy) eylemlere minimum seçim olasılığı verilir, \(\frac{\epsilon}{\mid A(s)\mid}\), ve olasılığın \((1-\epsilon)+\frac{\epsilon}{\mid A(s)\mid}\) büyüklüğü, açgözlü (greedy) eyleme verilir. \(\epsilon\)-açgözlü politikalar, tüm durumlar ve eylemler için bazı \(\epsilon > 0\) olan politikalar olarak tanımlanan \(\pi(a\mid s) \geq \frac{\epsilon}{\mid A(s)\mid}\), \(\epsilon-soft\) politikaların örnekleridir. \(\epsilon-soft\) politikaların içinden, \(\epsilon-greedy\) politikalar açgözlülüğe en yakın olanlarıdır.
Monte Carlo kontrolünün genel fikri genelleştirilmiş politika iterasyonu (GPI) olmasıdır. Monte Carlo ES’de olduğu gibi, mevcut politika için eylem değeri işlevini tahmin etmek için ilk ziyaret Monte Carlo yöntemlerini kullanıyoruz. Ancak, başlangıçları keşfetme varsayımı olmaksızın, politikayı sadece mevcut değer işlevine göre açgözlü (greedy) olarak geliştiremeyiz, çünkü bu durum, aç gözlü olmayan (non-greedy) eylemlerin daha fazla araştırılmasını engelleyecektir. Politikamızdaki yöntemde, yalnızca \(\epsilon\)-açgözlü bir politikaya taşıyacağız. Herhangi bir \(\epsilon\)-yumuşak politika için, \(\pi\), \(q\) ile ilgili herhangi bir \(\epsilon\)-açgözlü politika \(\pi\)‘den daha iyi veya eşit olması kesindir.
Aynı eylem ve durumun orijinali olarak ayarlanmış olan bir çevre düşünürsek eğer, durumlardan da aksiyon alınıyorsa, yeni çevre o zaman olasılığı \(1 - \epsilon\) ile eski ortamdaki gibi davranır. Bu olasılıkta eylem, rastgele eşit olasılıklarla tekrar eder ve daha sonra yeni, rastgele eylemle eski ortamdaki gibi davranır. Bu yeni ortamda genel politikalarla yapabilecek en iyi durumdur, yani orijinal ortamda \(\epsilon-soft\) politikalar ile yapılabilecek en iyi olanın aynısıdır. \(V\) ve \(q\) yeni ortam için en uygun değer fonksiyonlarını gösterir. Daha sonra bir politika \(\pi, \epsilon-soft\) politikaları arasında ve sadece \(\tilde{v_*}(s)\) = \({v_\pi}(s)\) ise en uygun olandır. \(\tilde{v_*}(s)\)’ in tanımından,
\[\begin{align*} \tilde{v_{*}}(s) &= (1-\epsilon)\max_a \tilde{q_{*}}(s,a) + \dfrac{\epsilon}{|A(s)|} + \displaystyle\sum_a \tilde{q_{*}}(s,a) \\ &= (1-\epsilon)\max_a \displaystyle\sum_s p(s',r|s,a)[r+ \gamma\ \tilde{v_{*}}(s')]+ \dfrac{\epsilon}{|A(s)|} \displaystyle\sum_a \displaystyle\sum_{s',r} p(s',r|s,a)[r+ \gamma\ \tilde{v_{*}}(s')] \end{align*}\]Yukarıdaki eşitlikten ve \(\epsilon-soft\) politika \(\pi\) artık geliştirildiğinde ise,
\[\begin{align*} v_\pi(s)&= (1-\epsilon)\max\limits_a q_\pi(s,a)+ \dfrac{\epsilon}{|A(s)|} \sum_a q_\pi(s,a) \\ &= (1-\epsilon)\max_a \sum_{s',r} p(s',r|s,a)\big[r+ \gamma v_\pi(s')\big] + \dfrac{\epsilon}{|A(s)|}+ \sum_a \sum_{s',r} p(s',r|s,a)\big[r+ \gamma v_\pi(s')\big] \end{align*}\]Bununla birlikte, bu denklem, \(v_\pi\)’ nin \(v_*\) ile yer değiştirmesi haricinde, bir öncekiyle aynıdır. Özet olarak, politika iterasyonunun \(\epsilon-soft\) politikalar için çalıştığını gösterdik. \(\epsilon-soft\) politikalar için açgözlü (greedy) politikanın doğal düşüncesini kullanarak, \(\epsilon-soft\) politikalar arasında en iyi politikanın bulunmadığı durumlar dışında her adımda iyi olduğunu gördük. En önemlisi de başlangıçları keşfetme varsayımını ortadan kaldırmış olduk.
Önem Örneklemesi ile Politika Dışı Tahmin (Off-Policy Prediction via Importance Sampling)
Tüm öğrenme kontrol yöntemleri bir ikilemle yüzleşir: Daha sonraki optimal davranışa göre eylem-değerlerini öğrenmeye çalışırlar, ancak optimal eylemleri bulmak için optimal olmayan davranışlarda bulunması gerekir. Keşif politikası bir uzlaşmadır ve hala araştırılan en uygun politika için eylem değerlerini öğrenir. Daha basit bir yaklaşım ise iki politika kullanmaktır; bunlar, öğrenilen ve en uygun politika haline gelen hedef politika ile keşif yapan ve davranış üretmek için kullanılan davranış politikasıdır. Bu durumda öğrenme, hedef politikada “kapalı” veriden (data “off”) olduğunu ve genel sürecin “politika-dışı öğrenme” (off-policy) olarak adlandırıldığını söyleyebiriz.
Politika-dışı yöntemler daha güçlü ve geneldir. Hedef ve davranış politikalarının aynı olduğu özel durum olarak politika üstü yöntemleri içerir. Politika dışı yöntemler ayrıca uygulamalarda çeşitli ek kullanımlara sahiptir. Örneğin, geleneksel bir öğrenme kontrolörünün veya bir insan uzmanının ürettiği verilerden öğrenmek için sıklıkla uygulanabilirler. Politika dışı öğrenme, gerçek dünya dinamiklerinin çok adımlı (multi-step) tahmin modelleriyle öğrenmenin anahtarı olarak görülmektedir
Bu bölümde, hem hedef hem de davranış politikalarının sabit olduğu tahmin problemini göz önüne alarak, politika dışı yöntemlere başlıyoruz. Yani, \(v_{\pi}\) veya \(q_{\pi}\)’yi tahmin etmek istediğimizi varsayalım, fakat sahip olduğumuz tek şey, başka bir politika izleyen bölümlerimizde \(b\), \(b \neq \pi\)’dir. Bu durumda \(\pi\) hedef politikadır (target policy) , \(b\) davranış politikasıdır (behavior policy) ve her iki politikada kararlaştırılır ve karar verilir.
Hedef politika \(\pi\) için değerleri tahmin etmek amacıyla davranış politika \(b\)’den bölümleri kullanırız, \(\pi\) ile alınan her eylemin, en azından bazen \(b\)’ nin altında kalmasını talep ederiz. Davranış politikasının (\(b\)), hedef politika (\(\pi\)) ile özdeş olmayan durumlarda stokastik (rastlantısal) olması gerekir. Öte yandan, hedef politika \(\pi\), deterministik olabilir ve aslında, bu, kontrol uygulamalarında özel bir ilgidir. Kontrolde, hedef politika genellikle eylem-değer fonksiyonunun mevcut tahminine göre belirleyici açgözlü politikadır. Davranış politikasının stokastik ve daha keşifçi, örneğin ε-açgözlü bir politika olduğu halde, bu politika belirleyici bir en uygun politika haline gelir. Ancak bu bölümde, hedef politikasının \(\pi\)‘nin değişmediği ve verildiği tahmin problemini ele alıyoruz.
Politika-dışı yöntemler, bir örneklemden diğerine örnek verilen dağıtım altında, beklenen değerlerin tahmin edilmesi için genel bir teknik olan önem örneklemini (Importance Sampling) kullanmaktadır. Önem örnekleme oranı (importance-sampling ratio), hedefin altında gerçekleşen yörüngelerin nispi olasılığına ve önem örnekleme oranı olarak adlandırılan davranış politikalarına göre, verimsiz geri kazanma yoluyla önem örneklemesi uygularız. Bir \(S_{t}\) başlangıç durumu verildiğinde, sonraki durum-eylem yörüngesinin olasılığı, \(A_{t},S_{t+1},A_{t+1},...S_{T}\), herhangi bir politika altında gerçekleşiyor \(\pi\),
\[\begin{align*} &Pr\{ {A_t, S_{t+1},A_{t+1},...,S_T | S_t,A_{t:T-1}\sim \pi}\} \\ &= \pi (A_t|S_t)p(S_{t+1}|S_t,A_t)\pi(A_{t+1}|S_{t+1})...p(S_T|S_{T-1},A_{T-1}) \\ &= \prod_{k=t}^{T-1} \pi (A_k|S_k)p(S_{k+1}|S_k,A_k) \end{align*}\]Burada \(p\)’nin durum-geçiş olasılığı fonksiyonu (state-transition probability function) olduğunu hatırlayalım . Bu nedenle, yörüngenin hedef ve davranış politikaları altındaki göreceli olasılığı (önem örnekleme oranı),
\begin{align} \rho_{t:T-1}\doteq \frac{\prod_{k=t}^{T-1} \pi (A_k|S_k)p(S_{k+1}|S_k,A_k)}{\prod_{k=t}^{T-1} b (A_k|S_k)p(S_{k+1}|S_k,A_k)} =\prod_{k=t}^{T-1} \frac{\pi (A_k|S_k)}{b(A_k|S_k)} \qquad (5.3) \label{eq:53} \end{align}
Hedef politika kapsamında beklenen dönüşleri (değerleri) tahmin etmek istediğimizi hatırlayın, ancak sahip olduğumuz tek şey davranış politikası nedeniyle \(G_{t}\) değerini döndürür. Bu dönüşler, \(\mathbb{E}[G_{t}\mid S_{t}=s]=v_{b}(s)\) ‘nin yanlış beklentisine sahiptir ve bu nedenle, \(v_{\pi}\)’yi elde etmek için ortalaması alınamaz. Bu, örneklemenin önem kazandığı yerdir. \(\rho_{t:T-1}\) oranı, dönüşleri, beklenen doğru değere dönüştürür:
\begin{align} \mathbb{E}[p_{t:T-1}G_{t}|S_{t}=s]= v_{\pi}(s) \qquad (5.4) \end{align}
Şimdi, \(v_{\pi}(s)\) değerini tahmin etmek için politika \(b\)‘yi izleyen, gözlemlenen bölümlerden oluşan bir gruptan ortalamaları döndüren bir Monte Carlo algoritması vermeye hazırız. Burada, bölüm sınırlarının ötesine geçen bir şekilde zaman basamaklarını saymak uygun olur. Yani, yığının ilk bölümü 100 zamanında bir uç(terminal) durumunda bitiyorsa, sonraki bölüm t = 101 zamanında başlar. Bu, belirli bölümlerdeki belirli adımlara başvurmak için zaman adımı sayılarını kullanmamızı sağlar. Özellikle, durumların ziyaret edildiği, \(T(s)\)olarak gösterilen tüm zaman adımlarının kümesini tanımlayabiliriz. Bu her ziyaret için bir yöntemdir; \(\tau(s)\) sadece bölümlerin içinde ilk kez ziyaret edilen zaman adımlarını içerecektir. Ayrıca, \(T_{t}\)‘nin t zamanını takip eden ilk bitiş(termination) süresini gösterir ve \(G_{t}\), \(T_{t}\)’ den sonra t geri dönüşü gösterir. Daha sonra \(\left\{G_{t}\right\}_{t\epsilon \tau(s)}\) leri duruma ait iadelerdir ve \(\left\{ \rho_{t:T(T)-1}\right\}_{t\epsilon \tau(t)}\) karşılık gelen önem örnekleme oranlarıdır. \(v_{\pi}(s)\) değerini tahmin etmek için, yalnızca getirileri oranlara göre ölçeklendirir ve sonuçları ortalarız:
\begin{align} V(s)\dot {=} \frac{\sum_{t\in\mathcal{T}(s)}\rho_{t:T(t)-1}G_t}{\mid\mathcal{T}(s)\mid} \qquad(5.5) \end{align}
Önem örnekleme bu şekilde basit bir ortalama olarak yapıldığında, sıradan önem örnekleme (ordinary importance sampling) denir. Önemli bir alternatif olarak, ağırlıklı ortalama kullanan ağırlıklı önem örneklemesi ( weighted importance sampling) aşağıdaki gibi tanımlanır,
\begin{align} %%\mathcal’ın aslında \mathfrak olması gerekiyor ama çalışmıyor paketi olmadığından V(s) \dot{=} \frac{\sum_{t\in\mathcal{T}(s)}\rho_{t:T(t)-1}G_t}{\sum_{t\in\mathcal{T}(s)}\rho_{t:T(t)-1}} \qquad (5.6) \end{align}
veya payda sıfır ise sıfır olur. Bu iki örneklemenin önemini anlamak için, ilk-ziyaret yöntemlerinin tahminlerini, durumdan tek bir dönüşü gözlemledikten sonra dikkate alın. Ağırlıklı ortalama tahminde, tek getiri için \(\rho_{t:T(T)-1}\) oranı, pay ve paydada iptal eder, böylece tahmin, orandan bağımsız olarak gözlemlenen dönüşe eşittir (oranın sıfırdan farklı olduğu varsayılarak). Bu geri dönüşün gözlenen tek şey olduğu göz önüne alındığında, bu makul bir tahmindir, ancak beklentisi \(v_{\pi}\) yerine \(v_{b}(s)\) dir ve bu istatistiksel anlamda ön yargılıdır. Aksine, sıradan önem-örnekleme tahmincisinin \((5.5)\) ilk ziyaret versiyonu, beklenti içinde her zaman \(v_{\pi}(s)\) olur, fakat bu aşırı olabilir. Oranın on olduğunu göz önünde bulundurun, gözlemlenen yörüngenin davranış politikası kapsamında olduğu gibi, hedef politikaya göre on kat daha fazla olduğunu gösterir. Bu durumda, sıradan önem-örnekleme tahmini, gözlemlenen geri dönüşün on katı olacaktır. Yani, bölümün yörüngesinin hedef politikayı çok iyi temsil ettiği düşünülse de gözlemlenen getiriden oldukça uzak olacaktır.
Formal olarak iki tür önem örneklemesi arasındaki fark önyargıları(bias) ve varyansları ile ifade edilir.
Sıradan önem örneklemesi
- Önyargısızdır.
- Varyansı genel olarak sınırsızdır çünkü oranların varyansı sınırsız olabilir.
Ağırlıklı önem-örneklemesi
- Önyargılıdır. (Önyargı asimptotik olarak sıfıra yakınlaşır)
- Herhangi bir tek geri dönüşteki en büyük ağırlık bir olacağı için varyansı sınırlıdır. (sınırlı geri dönüşler varsayıldığında, oranların varyansı sonsuz olsa bile, ağırlıklı önemlilik örneklemesi tahmincisinin varyansı sıfıra yaklaşmaktadır.
Pratikte, ağırlıklı önem örneklemesi büyük ölçüde daha düşük varyansa sahiptir ve kuvvetle tercih edilir. Fakat her iki önem örneklemesine yönelik her ziyaret (the every-visit) metodları her ikisi içinde önyargılıdır, yine de, örnek sayısı arttıkça önyargı, asimptotik olarak sıfıra düşmektedir. Pratikte, her ziyaret metotları sıklıkla tercih edilir, çünkü hangi durumların ziyaret edildiğini takip etme ihtiyacını ortadan kaldırırlar çünkü yaklaşık değerlere uzanmaları çok daha kolaydır.
Örnek 5.4 :Blackjack Durum Değerinin Politika Dışı Tahmini (Blackjack, yirmibir oyunu diye geçer. Kart oyunudur.) Tek bir blackjack durumunun değerini (Örnek 5.1), politika dışı verilerden tahmin etmek için hem normal hem de ağırlıklı önem örnekleme yöntemlerini uyguladık. Monte Carlo yöntemlerinin avantajlarından biri, tek bir durumu değerlendirmek için kullanılabilmesi. Bu örnekte, dağıtıcının bir zar gösterdiği durumu, oyuncunun kartlarının toplamının 13 olduğunu ve oyuncunun kullanılabilir bir ası olduğunu değerlendirdik (yani, oyuncu bir as ve bir zar yada eşdeğerde üç as tutar ). Veriler bu durumdan başlayarak oluşturulduktan sonra vurmayı seçer veya eşit olasılıkla( davranış politikası) rastegele kartı atar. Hedef politika, Örnek 5.1’de olduğu gibi, sadece 20 veya 21’lik bir tutara dayanmakta. Bu politikanın hedef politikaya göre değeri yaklaşık 0.27726’dır.Her iki politika dışı yöntem de, rastgele politika kullanılarak 1000 politika dışı bölümden sonra bu değere yakın bir şekilde yaklaştı. Şekil 5.3 bize iki yöntemin değerlendirilmesi hakkında bilgi verir.
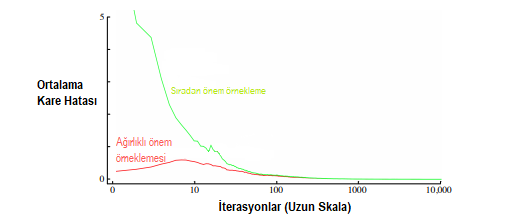
Şekil 5.3 :Ağırlıklandırılmış önem örneklemesi, politika dışı bölümlerden alınan tek bir blackjack durumunun daha düşük hata tahminleri üretir.
Örnek 5.5 :Sonsuz Varyans Sıradan önem-örneklemesine sahip tahminlerin tipik olarak sonsuz varyansa sahip olduğunda bahsetmiştik. Dolayısıyla tatmin edici olmayan yakınsama özelliklerine sahip olacaktır. Ne zaman, yörüngede ölçeklendirilmiş sonsuz varyansa sahip dönüşler bulunduğunda politika dışı öğrenmede kolaylıkla gerçekleşebilir. Şekil 5.4’te basit bir örnek gösterilmiştir.
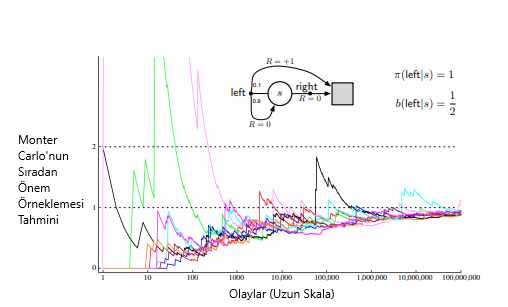
Şekil 5.4 :(Örnek 5.5) için sıradan önem-örneklemesi, tek durumlu MDP ile gösterilen görsel üzerinde şaşırtıcı derecede kararsız tahminler üretmektedir . Buradaki doğru tahmin 1’dir (γ = 1), ve bu örnek bir dönüşün beklenen değeri (önem örneklemeden sonra) olsa bile, örneklerin varyansı sonsuzdur ve tahminler bu değere yaklaşmaz. Bu sonuçlar politika dışı ilk ziyaret Monte Carlo İçindir.
Milyonlarca bölümden sonra bile, tahminler 1’in doğru değerine yakınsamamaktadır. Aksine, ağırlıklı önem örnekleme algoritması, sol hareketle sona eren ilk bölümden sonra sonsuza kadar tam olarak bir tahmin verecektir. 1’e (yani, doğru eylemle biten) eşit olmayan tüm dönüşler, hedef politika ile tutarsız olur ve bu nedenle sıfırdan bir \(p_{t:T(t)-1}\)’e sahip olur ve ne paydada ne de payda (5.6)’ya katkıda bulunmaz. Ağırlıklandırılmış önem örnekleme algoritması, yalnızca hedef politika ile tutarlı dönüşlerin ağırlıklı bir ortalamasını üretir ve bunların tümü tam olarak 1 olur.
Ölçekli önem örneklemeli dönüşlerin varyansının bu örnekte basit bir hesaplama ile sınırsız olduğunu doğrulayabiliriz. Herhangi bir rastgele değişken X’in varyansı, yazılabilen ortalama \(\bar{X}\) sapmanın beklenen değeridir,
\begin{align} Var[X]\dot{=} \mathbb{E}\big[(X-\bar{X})^2 \big] = \mathbb{E}[{X ^ 2}-2X\bar{X}+ \bar{X}^2] = \mathbb{E}[{X^2}]- \bar{X}^2 \end{align}
Dolayısıyla, eğer ortalama, sonlu ise, bizim durumumuzda olduğu gibi, varyans sonsuzda ancak ve ancak rastgele değişkenin karesinin beklentisi sonsuzdur. Bu nedenle, yalnızca örnekleme ölçekli dönüşün öneminin beklenen karesinin sonsuz olduğunu göstermemiz gerekir.
\begin{align} %”E” Fontu düzenlenecek. \mathbb{E_b} \Bigg[\bigg(\prod_{t=0}^{T-1} \frac{\pi(A_t|S_t)}{b(A_t|S_t)}G_0 \bigg)^ 2 \Bigg] . \end{align}
Bu beklentiyi hesaplamak için, bölüm uzunluğuna ve bitiş durumuna göre alt durumlara ayırıyoruz. İlk olarak, doğru eylemle biten herhangi bir bölüm için, önem örnekleme oranı sıfır olur, çünkü hedef politikanın bu eylemi asla gerçekleştirmez: Bu bölümler böylece beklentiye hiçbir şey katmaz (parantez içindeki miktar sıfır olacaktır) ve göz ardı edilebilir. Yalnızca uç dışı (non-terminal) duruma geri dönen sol eylemlerin bir kaç sayısını (muhtemelen sıfıra) içeren bölümleri ve sonlandırmaya geçen bir sol eylemi izlememiz gerekiyor. Tüm bu bölümlerin 1’i geri döndürür, bu yüzden \(G_{0}\) faktörü göz ardı edilebilir. Beklenen kareyi elde etmek için, sadece bölümün her bir uzunluğunu dikkate almalı, bölümün oluşumunun olasılığını önem örnekleme oranının karesiyle çarpmalı ve bunları ekleyelim:
\[\begin{align*} &=\displaystyle \frac{1}{2} *0.1 \bigg( \frac{1}{0.5} \bigg)^2 \\ &+\frac{1}{2}*0.9 * \frac{1}{2}* 0.1 \bigg( \frac{1}{0.5} \frac{1}{0.5}\bigg)^{2} \\ &+\frac{1}{2}*0.9 * \frac{1}{2}*0.9 * \frac{1}{2} * 0.1 \bigg( \frac{1}{0.5} \frac{1}{0.5} \frac{1}{0.5}\bigg)^2 \\ &+\ldots \\ &= 0.1 \sum_{k=0}^{\infty} 0.9^{k} * 2^{k} * 2 = 0.2 \sum_{k=0}^{\infty} 1.8^{k} = \infty . \end{align*}\]Kademeli Uygulama (Incremental Implementation)
Monte Carlo tahmin yöntemleri, Bölüm 2’de (Bölüm 2.4) anlatılan tekniklerin uzantıları kullanılarak, bölümler bazında, aşamalı olarak kullanılabilir. Bölüm 2’de ortalama ödülleri alırken Monte Carlo yöntemlerinde ise ortalama getiriyi elde ettik. Aynı metotları Monte Carlo yöntemleri içinde kullanabiliriz.
Sıradan önem örneklemede sonuçlar, örnekleme oranı \(\rho_{t=T(t)-1}\) Denklem 5.1 ile ölçeklendirilir, daha sonra (5.5) ‘de olduğu gibi basitçe ortalaması alınır.
\(G_1, G_2, ..., G_{n-1}\) halinde bir dizi olduğunu varsayalım. Hepsi aynı durumda ve her biri karşılık gelen rastgele bir ağırlık \(W_i,(W_i = \rho_{t=T(t)-1})\) ile başlar. Tahmini hesaplamak ister,
\(V_n \dot{=} \dfrac{\sum\limits_{k=1}^{n-1} W_k G_k}{\sum\limits_{k=1}^{n-1} W_k}, \qquad n \ge 2\) ve \(G_n\)’yi elde edene kadar tahmini güncel tutmamız gerekir. \(V_n\)’i güncellemenin yanı sıra n değerlerini kümülatif olarak topladığımız bir \(C_n\) değeri de olmalı. \(V_n\)’in güncelleme formülü ;
\[\begin{align*} V_{n+1} &\dot{=} V_n + \dfrac{W_n}{C_n} \big[G_n - Vn\big], n \ge 1 \qquad (5.8)\\ \\ C_{n+1} &\dot{=} C_n + W_{n+1} \\ C_0 &\dot{=} 0 \end{align*}\]Politika Dışı Monte Carlo Kontrol (Off-policy Monte Carlo Control)
Monte Carlo Kontrol Yöntemleri, daha önce bahsedilen tekniklerden birisini kullanır. Hedef politikayı öğrenirken ve geliştirirken davranış politikasını takip ederler. Bu teknikler, davranış politikasının, hedef politika (kapsam) tarafından seçilebilecek tüm eylemleri seçme olasılığının sıfır olması olasılığını gerektirir. Tüm olasılıkları keşfetmek için davranış politikasının yumuşak olmasını (yani, tüm durumlarda sıfır olmayan olasılıkla tüm eylemleri seçmesini) isteriz. Aşağıdaki şemada Monte Carlo Kontrol’ün tahmin için politika dışı öğrenimi gösterilmektedir.
Hedef politika \(\pi \approx \pi_*\), \(Q\) ye bağlı ve \(q_\pi\)’nin bir tahmini olan aç gözlü bir politikadır. Davranışsal politika \(b\) her şey olabilir, fakat politikanın en uygun politikaya yakınlaşmasını sağlamak için, her bir durum ve eylem çifti için sonsuz sayıda ödül elde etmek gerekir. Bu, \(\varepsilon-soft\) olmak için \(b\) seçilerek sağlanabilir. Politikalar, eylemler, bölümler arasında ve hatta bölümler içinde değişebilen farklı bir yumuşak politikaya \((b)\) göre seçilmiş olsa bile, karşılaşılan tüm durumlarda en uygun hale gelir.
Politika Dışı Monte Carlo Kontrol, tahmin için \(\pi \approx \pi_*\) Başlıyoruz, hepsi için \(\mathcal{s \in S , a \in A(s):}\)
\(Q(s,a) \in \mathbb{R}\) (İsteğe bağlı) \(C(s,a) \gets 0\) \(\pi(s) \gets argmax_a Q(s,a)\)
Sonsuz Döngü (Her bölüm için)
\(b \gets\) Herhangi bir yumuşak politika
\(b\)’yi kullanarak bir bölüm oluşturun \(b: S_0,A_0,R_1,...,S_{T-1},A_{T-1},R_T\)
\(G \gets 0\)
\(W \gets 1\)
Bölümün her adımı için döngü, \(t=T-1,T-2,..,0:\)
\(G \gets \gamma G+R_{t+1}\)
\(C(S_t,A_t)\gets C(S_t,A_t) + W\)
\(Q(St,A_t) \gets Q(S_t,A_t) + \frac{W}{C(S_t,A_t)}[G-Q(S_t,A_t)]\)
\(\pi(S_t)\gets argmax_a Q(S_t,a)\)
Eğer, \(A_t \neq \pi(S_t)\) ise döngüden çık.
\(W \gets W \frac{1}{b(A_t | S_t)}\)
Potansiyel bir sorun olarak bu yöntemin yalnızca bölümdeki kalan tüm eylemlerin açgözlü olduğu bölümlerin kuyruklarından öğrenmesidir. Açgözlü olmayan eylemler yaygınsa, özellikle uzun bölümlerin erken bölümlerinde görünen durumlar için öğrenme yavaş olacaktır. Bu da büyük ölçüde öğrenmeyi yavaşlatabilir. Bu sorunun ne kadar önemli olduğunu değerlendirmek için politika dışı Monte Carlo yöntemleri ile yetersiz deneyim olmuştur. Bu durumu çözümü bir sonraki bölümde anlatılacak Zamansal-Fark Öğrenme (Temporal Difference) yöntemi ile çözülebilir.
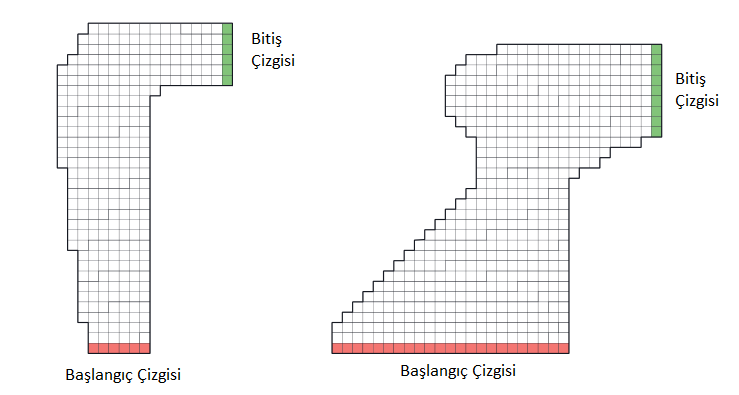
Şekil 5.5 : Yarış pisti görevi için birkaç sağa dönüş yapılır.
Alıştırma 5.12 : Yarış Pisti (programlama) : Şekil \(5.5\)‘de gösterilenler gibi bir yarış arabasını bir tur etrafında sürmeyi düşünün. Mümkün olduğu kadar çabuk gitmek istiyorsun, ama pistten kaçmak için o kadar hızlı değilsin. Basitleştirilmiş yarış pistimizde, araç, şematik göstergelerdeki ayrı bir dizi konumdan biridir. Hız ayrıca ayrıktır, zaman adımı başına yatay ve dikey olarak hareket eden bir dizi ızgara hücresi. Eylemler hız bileşenlerine artışlardır. Her adımda, her biri dokuz (3 × 3) eylem için +1, - 1 veya 0 ile değiştirilebilir. Her iki hız bileşeni de negatif olmayan ve 5’ten az olan ve başlangıç çizgisi hariç ikisi de sıfır olamaz. Her bölüm, her iki hız bileşeni sıfır ile rastgele seçilen başlangıç durumlarından birinde başlar ve araç bitiş çizgisini geçtiğinde sona erer. Ödüller, araba bitiş çizgisini geçene kadar her adım için 1’dir. Eğer araç palet sınırına ulaşırsa, başlangıç çizgisinde rastgele bir konuma geri taşınırsa, her iki hız bileşeni de sıfıra indirilir ve bölüm devam eder. Aracın konumunu her zaman adımında güncellemeden önce, aracın öngörülen yolunun parkur sınırını kestirip kestiğini kontrol edin. Bitiş çizgisini kesişirse bölüm sonlanır; Başka bir yerde kesişirse, aracın pist sınırına çarptığı ve başlangıç çizgisine geri gönderildiği kabul edilir. Görevi daha zorlu hale getirmek için, her bir zaman adımında olasılıkla (0.1), hız artışları, istenen artışlardan bağımsız olarak sıfırdır. Her başlangıç durumundan optimal politikayı hesaplamak için bu göreve Monte Carlo kontrol yöntemi uygulayın. Optimal politikayı izleyen çeşitli yörüngeleri sergilemek (ancak bu yörüngeler için gürültüyü kapatmak).
