Pekiştirmeli Öğrenme - Bölüm 3: Sonlu Markov Karar Süreçleri
Sonlu Markov Karar Süreçleri
Markov Karar Süreçleri (Markov Decision Processes), eylemlerin sadece bir sonraki ödülü değil gelecek durumları da etkilediği sıralı karar verme sürecinin klasik bir formülasyonudur. Aynı zamanda Pekiştirmeli Öğrenme probleminin matematiksel olarak idealleştirilmiş biçimleridir. Bu bölümde, dönüş değerleri, değer fonksiyonları ve Bellman denklemlerinden bahsedilecektir.
Ajan-Çevre Arayüzü (The Agent-Environment Interface)
Pekiştirmeli Öğrenme’de veya Markov Karar Süreçleri’nde öğrenen ve karar veren elemana ajan denir. Bu ajanın etrafını kapsayan ve onun etkileşimde bulunabileceği her şeyi içinde barındıran alana ise çevre denir. Çevre, ajanın eylemlerine karşılık gelen ödülü verir ve ajan için eylem alması gereken yeni bir durum oluşturur. Bu şekilde, çevre ve ajan ikisi sürekli etkileşim halinde kalır. Bu etkileşime aşağıdaki yörünge örnek verilebilir;
\begin{align} S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, \cdots, \end{align}
Sonlu Markov Karar Süreçleri’nde; durum, eylem ve ödül kümelerinin tamamı sonlu sayıda elemana sahiptir. Bu durumda \(S_t\) (durum) ve \(R_t\) (ödül) sadece bir önceki durum ve eyleme bağlı olan, çevrenin dinamikleri tarafından belirlenen, iyi tanımlanmış ayrık bir olasılık dağılıma sahiptir. Bu etkileşimin geçmiş durumlardan sadece bir önceki duruma bağlı olması, durumların geleceğe etki edebilecek tüm geçmiş ajan-çevre etkileşimlerini kapsaması sebebi ile olmaktadır. Durumların bu özelliğine Markov Niteliği (property) denir. Geçiş olasılıkları (transition probability) ve beklenen ödül (expected reward) gibi gereksinim duyulan bir çok değere, ortam dinamiklerinin bilgisine sahip olan fonksiyon \(p(s',r \mid s,a)\) şeklinde gösterilmektedir.
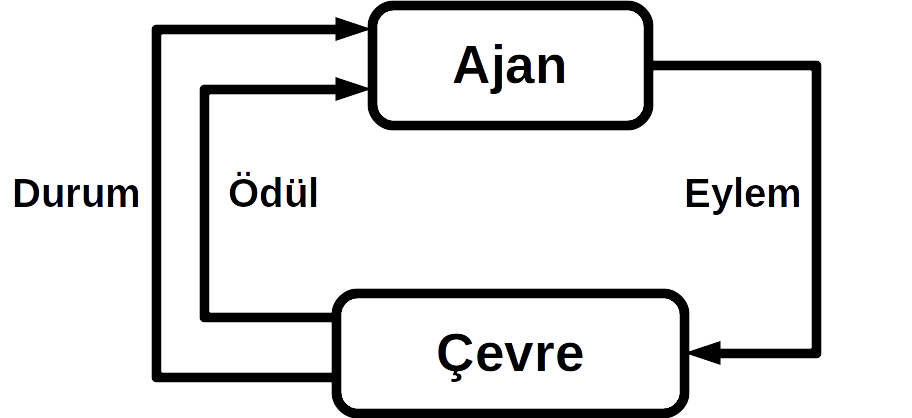
Sonuç olarak; Markov Karar Süreçleri’ne amaca yönelik, etkileşimle öğrenme probleminin kayda değer bir soyutlaştırması denilebilir. Markov karar süreçlerini özetler nitelikteki 3 işaret; ajanın aldığı kararları temsil eden eylemler, bu kararların alınma sebebini işaret eden durumlar ve ajanın hedefini gösteren ödül olmaktadır.
Hedefler ve Ödüller (Goals and Rewards)
Pekiştirmeli Öğrenme’de amaç, çevreden ajana daha fazla ödül aktarımının sağlanmasıdır. Ajanın seçtiği eylemler sonucunda elde ettiği ödül genellikle sayısal bir değer olmaktadır. Ajanın nihai hedefi ise uzun vadede toplam ödül miktarını en yüksek seviyeye ulaştırmaktır. Bu sistem ödül hipotezi (reward hypothesis) olarak isimlendirilmektedir.
Bir hedefi formüle etmek için ödül sinyalinin kullanılması Pekiştirmeli Öğrenme’nin ayırt edici özelliklerinden biridir. Ödül vesilesiyle, ajana yaptırılmak istenenin nasıl elde edilebileceğine dair önceden bilgi verilmesine gerek yoktur. Örneğin, satranç oynayan bir oyuncu kazanmak için ödüllendirilmelidir fakat rakibin taşlarını alarak yahut yönetim merkezinin kontrolünü ele geçirerek ödülü kazanmamalıdır. Eğer bu türden alt alanlara ulaşımı ödüllendirilirse, ajan gerçek hedefe ulaşmadan bunları başarmanın yolunu arayacaktır. Bu durum, rakibin taşlarını oyunu kaybetme pahasına almayı tercih etmeye yol açabilecektir. Ödül, nihai hedefe ulaştıracak sinyali temsil etmektedir.
Getiriler ve Olay (Returns and Episodes)
Ajanın eylemlerinden aldığı ödüller \({R_t, R_{t+1}, R_{t+2},}\cdots\) olarak belirtilirse aşağıdaki formülasyon ajanın kümülatif ödül değerini göstermektedir. Dolayısıyla ajanın hedefi \({G_t}\) değerini en yüksek seviyeye getirmeye çalışmaktır. Bu değere beklenen getiri (expected return) denilmektedir.
\begin{equation} \label{eq:31} {G_t} \dot {=} {R_{t+1}+R_{t+2}+R_{t+3}+ \cdots {+} {R_T}} \end{equation}
Ajan-Çevre etkileşimi, bölüm (episode) olarak isimlendirilen bir çok durum ve eylem serilerinden oluşan, uç durum denilen özel bir durum ile sona eren bir yapı ile sağlanmaktadır ve her bölüm sonunda durum tekrar başlangıç durumuna getirilmektedir. Bölümler birbirlerinden bağımsız olmaları sebebiyle her bölüm farklı ödül, durum ve eylemlerle sonuçlanabilir. Bir çok farklı problem içerisindeki Ajan-Çevre etkileşiminde ise yapı bölümlerden oluşmayabilir. Bu durumda, uç durum oluşmadığı için getiriler matematiksel olarak tanımlanmaktadır.
Ödül hesaplanırken ihtiyaç duyulan ek bir konsept ise indirim (discounting) olmaktadır. İndirim oranı (discount rate) kullanılarak azaltılan ödüllerin toplamı, indirimli getiriyi (discounted return) tanımlamaktadır. İndirim oranı \(\gamma\) ile gösterilmekte olup, 0 ile 1 arasında bir değer almaktadır.
\begin{equation} \label{eq:32} {G_t} \dot {=} {R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+ \cdots {=} \displaystyle\sum_{k=0}^\infty {\gamma^k}{R_{t+k+1}}} \end{equation}
İndirim oranı, gelecekteki ödüllerin karar anındaki önemini belirlemektedir. 0 olması durumunda ajan o andaki en yüksek ödülü alabilecek eylemi seçme eğilimindedir, parametre \(1'\)e yaklaştığı ölçüde ise gelecekteki ödülleri çok daha güçlü bir şekilde hesaba katarak eylemlerini seçmektedir. Bu oranın belirlenmesi ajanın öğrenimini doğrudan etkilemektedir.
Bölümlü ve Bölümsüz Problemler için Birleşik Notasyon (Unified Notation for Episodic and Continuing Tasks)
Önceki kısımlarda, ajan-çevre etkileşimi bölümlü ve bölümsüz olmak üzere iki türe ayrılmıştır. Bölümlü problemler matematiksel olarak daha kolay olmaktadır, zira her bir eylem sadece bölüm sırasında alınan sınırlı sayıda ödülü etkilemektedir. Problemleri çözerken iki tür problem yapısı da düşünülmeli ve her iki durumu eş zamanlı olarak sembolize edilebilecek bir gösterim tanımlanmalıdır.
Bölümlü problemler konusunda kesin bir yargıya varmak için ek bir gösterim gerekmektedir. Bu gösterim uzun tek bir zaman adımları (time steps) dizisinden ziyade her biri sonlu zaman adımı dizilerinden oluşan bir bölüm dizisi olarak düşünülmektedir. Sıfırdan başlayarak her bir bölümün zaman adımları numaralandırılmaktadır. \(S_t\), \(t\) zamandaki durumu temsil etmektedir. Fakat \(S_{t,i}\), \(i\)‘ci bölümün \(t\) zamanındaki durumu göstermektedir. Bölümlü problemlere bakıldığında, farklı bölümler arasında ayrım yapılmamaktadır. Bazen, özel bir bölüm ya da tüm bölümler için gösterimin doğru olduğu düşünülmekte olup \(S_{t,i}\) kullanılması gerekirken \(S_t\) kullanılmaktadır.
Politikalar ve Değer Fonksiyonları (Policies and Value Functions)
Hem bölümlü hem de bölümsüz problemleri kapsayan tek bir gösterim elde etmek için başka bir yönteme ihtiyaç duyulmaktadır. Denklem 3.1 getiriyi sınırlı sayıda terim üzerinden, Denklem 3.2 ise sonsuz sayıda terim üzerinden hesaplamaktadır. Bu iki denklem, yalnızca kendisine geçiş yapan ve sıfır ödül üreten özel bir durduran durumun kullanılması ile birleştirilebilir. Bu gösterimin diyagramı Şekil 3.2’de görülebilir.
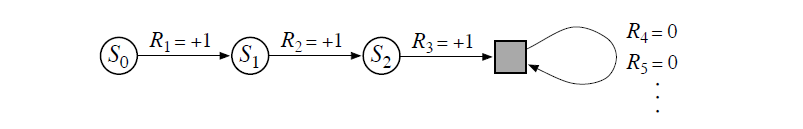
Şekildeki son durum (gri renkteki kare) bölümün sonuna karşılık gelen uç (terminal) durumu temsil eder. \(S_0\)’dan başlayarak ödül dizisi \(+1,+1,+1,0,0\) olarak görülür. \(T=3\) zamanında yahut sonsuz eylem adımı sonucunda ödülleri topladığımızda aynı getiri elde edilmektedir. Denklem 3.3’de indirimli formülasyon görülebilir.
\begin{equation} \label{eq:33} G_t \doteq \sum_{k = t + 1}^T \gamma^{k - t - 1} R_k \end{equation}
Politikalar ve Değer Fonksiyonları (Policies and Value Functions)
Hemen hemen tüm Pekiştirmeli Öğrenme algoritmaları, durumların ajan için ne kadar önemli olduğu gösteren değer fonksiyonlarının tahminlemesini kullanmaktadır. Bu değer fonksiyonları ise politika denilen, hangi eylemlerin seçileceğini olasılıksal olarak belirleyen sistemler vasıtası ile hesaplanmaktadır. Politika \(\pi\) kullanılarak gösterilirse, \(s\) durumlarına karşılık gelen, \(a\) eylem dağılımlarının gösterimi \(\pi(a|s)\) olmaktadır.
Politikaya bağlı olarak atılan adımlar ile elde edilen durumlar ve ödüllerden durum değer ve eylem değer fonksiyonları tahminlenmektedir. Durum değer fonksiyonu Denklem 3.3’de eylem değer fonksiyonu ise Denklem 3.4’de gösterilmiştir.
\[v_\pi(s) \dot{=} \mathbb{E}_\pi[G_t|S_t=s] = \mathbb{E}_\pi\bigg[\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg| S_t=s\bigg]\] \[q_\pi(s|a) \dot{=} \mathbb{E}_\pi[G_t|S_t=s,A_t=a] = \mathbb{E}_\pi\bigg[\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg| S_t=s,A_t=a\bigg]\]Durum-değer fonksiyonu \(s\) durumunda iken \(\pi\) politikası takip edildiğinde \(s\) durumunun beklenen değerini verir. Eylem-değer fonksiyonu ise \(s\) durumunda iken \(a\) eylemini \(\pi\) politikasını kullanarak seçtiğinde, durum-eylem ikilisinin beklenen değerini verir. İdealde \(\pi\) politikasına bağlı olarak erişilen herhangi bir durumdaki getiri, durum değer fonksiyonunun tahminine; seçilen eylem sonrasında hesaplanan getiri de, eylem değer fonksiyonunun tahminlemesine eşit olmalıdır.
Herhangi bir politika \(\pi\) ve durum \(s\) için, denklem 3.4’de \(s\) durumunun değeri ve \(s\)‘ten erişilebilecek durumların değeri arasındaki tutarlılık koşulunu göstermektedir. Bu denklem Bellman eşitliğini vermektedir.
\begin{equation} \label{eq:34} \displaystyle\sum_a \pi(a|s)\displaystyle\sum_{s’,r}p(s’,r|s,a)\bigg[r+\gamma v_\pi(s’)\bigg] \end{equation}
En Uygun Politikalar ve En Uygun Değer Fonksiyonları (Optimal Policies and Optimal Value Functions)
Her zaman diğer politikalardan üstün (kümülatif getirisi yüksek) veya eşit bir politika vardır ve bu politika, optimal yani en uygun politika olarak isimlendirilir. En uygun politika, en uygun durum-değer ve eylem-değer fonksiyonlarına sahip olmaktadır. En uygun politika \(\pi_*\) ile, en uygun durum-değer fonksiyonu \(v_*\) ile, en uygun eylem-değer fonksiyonu ise \(q_*\) ile gösterilmektedir. \(v_*\) durum-değer fonksiyonu için beklenen getiri hesabı Denklem 3.5’te verilmiştir. Bu denklem Bellman uygunluk eşitliğidir. Aynı eşitlik \(q_*\) eylem-değer fonksiyonu için de geçerlidir ve Denklem 3.6’da verilmiştir.
\[\label{eq:35} v_*(s) = \max_a\displaystyle\sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')]\] \[\label{eq:36} q_*(s,a) = \max_a\displaystyle\sum_{s',r}p(s',r|s,a)[r+\gamma\max_a' q_*(s',a')]\]En Uygunluk Ölçütü ve Yaklaşım (Optimality and Approximation)
Pekiştirmeli Öğrenme’de ilgilenilen problemlerde en uygun politika ve değer fonksiyonlarına ulaşmak çok büyük hesaplama maliyetleri oluşturabilir. Ortam dinamiklerinin doğru ve tam bir modeline sahip olunsa dahi, Bellman uygunluk eşitliği ile en uygun politikayı hesaplamak genellikle mümkün olmaz. Hesaplama maliyeti ile beraber, hafıza da önemli bir kısıtlama olmaktadır. Değer fonksiyonlarının, politikaların ve modellerin yaklaşımlarını oluşturmak çok büyük miktarlarda bellek gerektirebilmektedir.
Bu sebeple, problemlere belli hata payları ile yaklaşıklıklar ile yapılmaktadır. İşe yarar bir politikanın, en uygun politika olmamakla beraber belli bir kriter içerisinde seyretmesi, kullanılabilir bir yapıya dönüşebilir.
Pekiştirmeli öğrenmenin çevrimiçi (online) yapısı; daha az sıklıkla karşılaşılan durumlara daha az efor sarf ederek, sıkça karşılaşılan durumlarda daha iyi kararlar alması için en uygun politikaya yaklaşım yaptırmaya imkan sağlar. Bu, Pekiştirmeli Öğrenmeyi, MDP’leri yaklaşık olarak çözen diğer yaklaşımlardan ayıran önemli bir özelliktir.
