Pekiştirmeli Öğrenme - Bölüm 2: Çok Kollu Haydutlar
Çok Kollu Haydutlar
Pekiştirmeli öğrenmeyi diğer öğrenme modellerinden ayıran en önemli özellik; atılan eylem adımlarını, en uygun eylemlerin talimatları ile değerlendiren eğitim bilgilerini kullanmasıdır. Bu durum aktif araştırma yani iyi davranış için açık şekilde aramayı gerektirir.
Çok kollu haydutlar (multi armed bandits), pekiştirmeli öğrenmenin ayırt edici özelliğidir. Olasılık teorisindeki bir problemi ifade eden düşünce deneyi olarak tanımlanırlar. Diğer bir ifade ile bir karşılaştırma ya da sıralamada en yüksek kazancın nasıl elde edilebileceğine dair soru işaretlerine cevap olabilen bir yöntemdir.
\(k\)-kollu Haydut Problemi
Bu problem, pekiştirmeli öğrenmede en basit problem olarak bilinmektedir. Yapılan her seçimden, belli bir ortalamaya sahip rastgele bir dağılımdan seçilen eyleme (çekilen kol) bağlı olarak ödül alınmaktadır. Hedef ise toplam ödülü maksimum seviyeye ulaştırarak makineden en iyi kazancı sağlamaktır. Bu durum \(k\)-kollu haydut probleminin temelidir. Farklı eylemlerin farklı ödüller vermesiyle ödüller en yüksek seviyeye ulaştırılır.
Örneğin; hastalar için deneysel tedavilerin her birinin bir kol olduğu varsayılırsa, bu kollar arasından seçim yapan bir doktor için tedavi seçimi, hastanın sağlığını belirleyici bir durum olup o tedavi için ödülü oluşturmaktadır.
\(k\)-kollu haydut probleminde, her eylemin ortalama bir ödülü bulunmaktadır. Eylem kararı verilmeye devam edildikçe alınan ödül yükseltilmeye çalışılır. Bu da ancak keşif ve sömürü yöntemlerini dengeleyerek elde edilebilir. Bu yazının devamında birkaç basit \(k\)-kollu haydut dengeleme yönteminden bahsedilecektir.
Eylem-Değer Yöntemleri
En basit eylem seçme yöntemi, oluşturduğumuz eylem değer fonksiyonunda bize en yüksek ödülü sağlayacak olan eylemi her defasında seçmektir. Seçilen değer, giriş yazımızda bahsedilen açgözlü (greedy) eylemlerden biridir. Eğer birden fazla açgözlü eylem varsa aralarında rastgele seçim yapılacaktır.
Açgözlü politika (greedy policy), var olan bilgiyi günceller ve iyileştirir ancak ortam hakkında daha fazla bilgi almamızı ve ortamı keşfetmemizi engeller. Ortamı keşfetmek ve daha iyi bir ödül mekanizmasını açığa çıkarmak için açgözlü politikaya olasılıksal bir değer (epsilon) ekleyip, o olasılık gerçekleştiğinde rastgele hareket etmek hedeflenmektedir. Bu politikaya \(\epsilon\)-açgözlü politika (epsilon greedy policy) denilmektedir. Eğer teorik olarak oyun bu şekilde sonsuz kere oynanırsa, bu algoritma oyunun her dinamiğini keşfetmeyi sağlayacak ve en uygun eylem değer fonksiyonuna ulaşılabilecektir.
10-kollu Test Ortamı
Şu ana kadar anlatılanların grafik üzerinde incelenmesi için öncelikle 10-kollu test ortamının tanımını yapmak gerekir. 10-kollu Test Ortamı, \(k\) değişkeninin 10 olduğu bir haydut probleminin 2000 kez test edilmesinden oluşan bir test ortamıdır. Eylem seçimleri 1’den 10’a kadar ilerleyen kol numaralarıdır.
Şekil \(2.1\)‘de görülen grafikteki gri alanlar, her koldan alınacak ortalama ödüllerdir ve dağılım, normal dağılıma göre hazırlanmıştır.
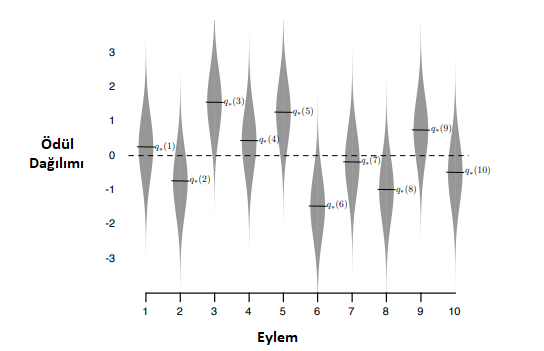
\(\quad\quad\)Şekil 2.1\(:\) Davranışların gerçek değerleri(siyah çizgiler) ve normal dağılıma göre dağıtılmış test sonuçları.
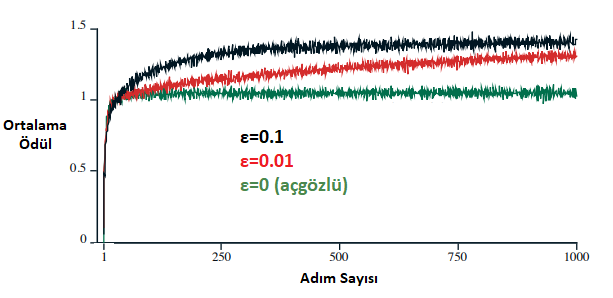
\(\quad\quad\quad\quad\qquad\)Şekil 2.2\(:\) Ortalama ödülün zamana göre dağılımı.
Şekil \(2.2\)‘de ise \(\epsilon\) değeri 0.01 ve 0.1 olan iki açgözlü olmayan, \(\epsilon\) değeri 0 olan ve açgözlü yaklaşım sergileyen 3 ajan bulunmaktadır. Bu ajanların 10-kollu Test ortamındaki ortalama performansları görülmektedir. Grafikte açgözlü yaklaşımın performansının ilk adımlarda arttığı, sonrasında ise keşfetmeyi durdurup ilk seferde eline geçen en verimli ödülü aldığı kolu çekmeye başladığını ve ödül artışının durduğu görülmektedir. Üstteki şekilde ulaşılan maksimum ortalama ödülün 1.5 civarında olduğunu, bunun sonucunda da açgözlü ajanın en yüksek performansın %65’i kadar verim alabildiği gözlemlenmektedir. Diğer 2 ajan ise açgözlü olmayan yaklaşımla keşfetmeyi devam ettirmişlerdir. Bu grafikte uzun süreçli eğitimlerde açgözlü olmayan yaklaşım, açgözlü yaklaşıma göre daha verimli olmuştur. \(\epsilon\)‘u 0.1 olan yaklaşım, 0.01 olan yaklaşıma göre 1000 adımlık süreçte daha iyi bir ödül kazanmış gibi görünse de performans oranında \(\epsilon\)‘u 0.01 olan ajan daha uzun sürecek bir koşuda daha iyi performans gösterecektir.
Eğer 1 olan varyans değeri daha da düşürülerek 0.1 yapılırsa, açgözlü olan davranışın en uygun ödülü bulup sonrasında keşfetmeyi durdurması sebebiyle, epsilonlu yaklaşıma göre daha verimli olacağı söylenebilir. Fakat varyans arttırılırsa, örneğin 10 yapılırsa, ödül dağılımı genişleyeceğinden her zaman keşfetmek diğer yaklaşıma göre daha verimli olacaktır. Bu sebeple bir çok problemde olduğu gibi Pekiştirmeli Öğrenme’nin en önemli meselelerinden biri olan keşfetme ve sömürü arasındaki dengeyi iyi sağlamak her zaman çok önemlidir.
Kademeli Uygulama
Şimdiye kadar anlatılan eylem-değer yöntemleri, tüm gözlemlenen ödülleri hafızada tutarak ve her adımda ortalamalarını alarak tahminde bulunmaktadır. Bu bölümde ortalamaların özellikle; bellek, zaman ve işlem yükü açısından verimli bir şekilde nasıl hesaplanabileceği aranmaktadır. Herhangi bir eylemin seçilmesinden sonra alınan ödülü \(R_i\) ve \(n-1\)’nci eylem için eylem değer tahminini \(Q_n\) göstermektedir.
\begin{equation} Q_n \stackrel{.}{=} \displaystyle\frac{R_1 + R_2 + … + R_{n-1}}{n-1} \end{equation}
Tüm ödüllerin kaydını tutmak bellek ve hesaplama gereksinimlerinin zamanla çok büyümesine sebebiyet verecektir. Her ek ödül, saklamak için ek bellek ve pay içindeki toplamı hesaplamak için ek hesaplamaya ihtiyaç duymaktadır. Tahmin edilebileceği gibi bu büyük işlem yüküne yol açmaktadır. Kademeli bir hesaplama yaparak bu problemin üstesinden gelmek mümkündür.
\(Q_{n + 1}= \displaystyle\frac{1}{n}\sum\limits_{i=1}^n R_i\) \(\)
\(= \dfrac{1}{n}\bigg(R_n + \sum_{i=1}^{n-1}R_i\bigg)\) \(\)
\(= \dfrac{1}{n}\bigg(R_n + (n-1)\frac{1}{n-1}\sum_{i=1}^{n-1}R_i\bigg)\) \(\)
\(= \dfrac{1}{n}\bigg(R_n + (n-1)Q_n\bigg)\) \(\)
\(= \dfrac{1}{n}\bigg(R_n + nQ_n - Q_n\bigg)\) \(\)
\(= Q_n + \dfrac{1}{n}\bigg[R_n - Q_n\bigg]\) \(\quad(2.3)\)
Bu şekilde bellek ve hesaplama yükünü azaltmış oluruz. Bu güncelleştirilmiş formül sıklıkla kullanılan bir formüldür. \([R_n - Q_n]\) değeri \(Q_{n+1}\) tahmininde hataya tekabül eder. Bu formülasyon kullanılarak, hedefe doğru bir adım atılır ve hata azaltılır.
Kademeli yöntemde kullanılan adım-boyu (step size) parametresinin her adımda değiştiğini unutmamak gerekir. Genellikle adım boyu parametresi bu yöntem için \(1/n\) olarak kullanır. Bu bölüm ve diğer bölümlerde, adım-boyu parametresi \(\alpha = 1/n\) veya daha genel olarak \(\alpha_t(a)=1/n\) şeklinde gösterilecektir.
Durağan Olmayan Problem Takibi
Bu noktaya kadar durağan haydut (stationary bandit) problemlerinin ortalama hesabına dayanan yöntemlerden bahsedildi. Bu yöntemler, ödül (reward) olasılıklarının zamanla değişmediği durağan problemler için uygundur. Ancak pekiştirmeli öğrenme problem uzayında durağan olmayan (non-stationary) problemlerle oldukça sık karşılaşılır. Bu tip problemlere yaklaşırken, yakın zaman eylemleri ile elde edilen ödül değerlerinin, daha geçmişteki eylemler ile elde edilen ödül değerlerine göre daha fazla ağırlıklandırılması, izlenilen başlıca yöntemler arasındadır. Mevzubahis problemin çözümü için, bir önceki bölümden farklı olarak \(\alpha\) değeri sabitlenebilir.
\begin{equation} Q_{n + 1} = Q_{n} + \alpha\bigg(R_n - Q_n\bigg), \qquad \alpha \in \left (0,1 \right ] \end{equation}
Buna istinaden; \(Q_{n + 1}\) tahmininde, geçmişteki tüm eylemlerin ödüllerini ve alınan ilk eylemin değer tahminini kapsayan aşağıdaki gibi bir ağırlandırma modeli kullanılabilir.
\begin{equation} Q_{n + 1} = (1-\alpha)^{n} Q_{1} + \sum_{i=1}^{n}\alpha(1-\alpha)^{n-i}R_i \end{equation}
Bu eşitliği inceleyecek olursak, \(1-\alpha\) değeri, 0 ile 1 arasında bir değer olacağından geçmişe gittikçe eşitliğe katılan geçmiş eylem ödüllerinin ağırlığı üstel bir şekilde azalmaktadır. Buna üstel yakın zaman ağırlıklı ortalama (exponential recency-weighted average) denilmektedir.
İyimser Başlangıç Değerleri
Başlangıç eylem değerleri, keşfi teşvik etmenin basit bir yolu olarak kullanılabilmektedir. Eylem değerlerini başlatırken sıfırlamak yerine, 10 kollu test ortamında yapıldığı gibi, ilk değerlerin 5 olarak ayarlanması, \(q_*(a)\) eylem-değer ortalamalarının 0 olduğu bir problem için çok iyimser bir yaklaşım olmaktadır. Ancak bu iyimserlik, yeni eylemleri keşfetmeye teşvik etmektedir. Başlangıçta hangi eylemler seçilirse seçilsin; ödül, başlangıç tahminlerinden daha az olacaktır; ajan eylemler sonucu alınan ödüller ile “hayal kırıklığı”na uğrayınca, diğer eylemleri deneyecektir. Bu sayede, tüm eylem çeşitleri değer tahminlerine yakınsamadan önce birkaç kez denenir. Her zaman açgözlü eylemler seçilmiş olsa dahi sistem neredeyse adil bir keşif yapacaktır. Şekil \(2.3\)‘te, tüm \(a\) değerleri için \(Q_1(a) = +5\) kullanılarak, açgözlü bir yöntemin 10 kollu haydut test ortamı üzerindeki performansı gösterilmektedir. Karşılaştırma için, ayrıca \(Q_1(a) = 0\) ile \(\epsilon-\)açgözlü bir yöntem gösterilmiştir.
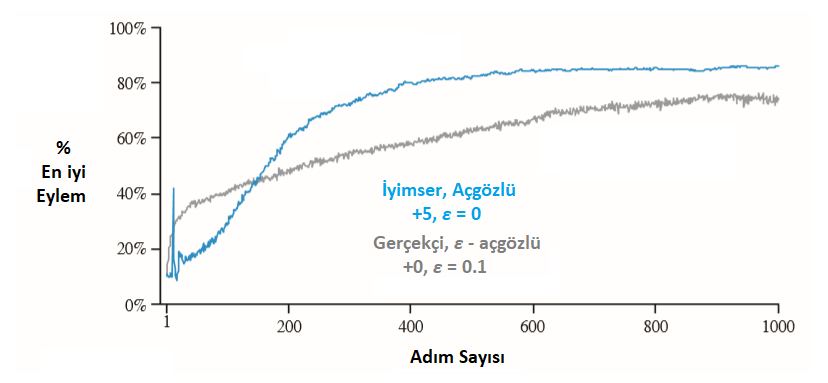Şekil 2.3 \(:\) İyimser başlangıç eylem değeri tahminlerinin 10 kollu test ortamı üzerindeki etkisi. Her iki yöntemde de sabit adım boyutu parametresi kullanılmıştır, \(\alpha=0.1\).
Başlangıçta, iyimser yöntemin keşfe ağırlık vermesi sebebiyle kötü bir performans sergilediği gözlemlenebilir. Fakat sonrasında, her eylem’i denemiş olması sebebiyle daha iyi sonuç vermektedir. Bu yöntem, durağan problemler üzerinde oldukça etkili olabilecek basit bir yaklaşım olmaktadır. Aksi durumda, yani durağan olmayan problemler için uygun olmamaktadır, zira bu yöntem yeni doğan bir ihtiyaca cevap olmaktan uzaktır. Genel olarak, başlangıç koşullarına odaklanmakta olan herhangi bir yöntemin durağan olmayan problemlere yardımcı olması olası değildir.
Üst-Güven-Sınırı Eylem Seçimi
Eylem-değerleri için her zaman bir belirsizlik olabileceği için keşif zorunlu olmaktadır. Açgözlü eylemler ilk bakışta avantajlı gibi görünse de, yapılacak bir keşifle daha iyi sonuçlar elde etmek mümkün olmaktadır. Bunu sağlamanın başka bir yolu da bu bölümde ele alınacaktır.
Üst-Güven-Sınırı (upper confidence bound) eylem seçimleri aşağıdaki formül \(2.4\)‘e göre yapılır.
\(A_t\dot{=}argmax\bigg[Q_t(a) + c\sqrt{\frac{\displaystyle lnt}{ N_t(a)}}\bigg]\quad\) \((2.4)\)
\(N_t(a), a\) eylemlerinin \(t\) zamanından önce seçilme sayısını gösterirken \(c\), arama derecesini kontrol eder. Eğer \(N_t(a) = 0\) olursa, \(a\) bir maksimizasyon eylemi olarak kabul edilir ve a eylemi bir sonraki eylem olarak seçilir. Üst-Güven-Sınırı eylem seçim fikri, karekökün, eylemin değer tahminindeki belirsizlik veya varyansının bir ölçütüdür. En üst sınıra çıkarılan \(a\)’nın olası gerçek değeri, c’nin güven düzeyini belirlemesiyle kontrol edilir. \(a\) eylemi her seçildiğinde belirsizlik büyük ihtimalle azaltılır; paydada görünen \(N_t(a)\) artışı belirsizliği azaltır. Diğer taraftan, her seferinde bir eylem seçildiğinde \(t\) artar, ancak \(N_t(a)\) paydada göründüğü için, belirsizlik tahmini artar. Doğal logaritmanın kullanılması, artışların zaman içinde küçüldüğü, ancak sınırsız olduğu anlamına gelir; Tüm eylemler sonunda seçilecektir, ancak daha düşük değer tahminlerine sahip veya daha önce seçilmiş olan eylemler zamanla azalan sıklıklarla seçilecektir.
10-kollu test setindeki Üst-Güven-Sınırı eylem seçiminin ortalama performansı Şekil \(2.4\)‘te gösterilmiştir.
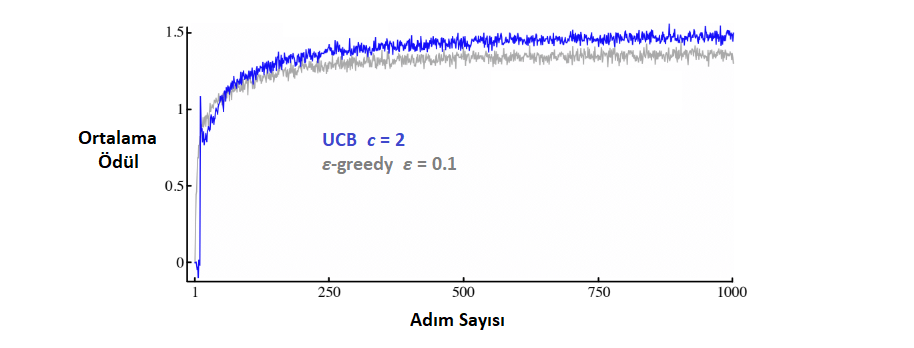
\(\quad\quad\quad\quad\qquad\)Şekil 2.4\(:\) Üst-Güven-Sınırı eylem seçiminin ortalama performansı.
Gradyen Haydut Algoritmaları
Bölümde şu ana kadar, eylem değerleri hesaplandı ve eylemleri seçmek için hesaplanan bu değerler kullanıldı. Bu bölüm ise eylemlerin seçimi için \(H_t(a)\) ile gösterilen sayısal bir tercih değeri kullanmaktadır. Bu tercih ne kadar yüksekse, o eylemin seçilme olasılığı o denli artmaktadır. Bu değerin hesabı ise, soft-max dağılımı ile yapılmaktadır.
\begin{equation} \pi_t(a) = \dfrac{e^{H_t(a)}}{\displaystyle \sum\limits_{b=1}^k e^{H_t(b)}} \end{equation}
\(\pi_t(a)\) değeri, \(a\) eylemi için \(t\) zamanındaki seçim olasılığını vermektedir. \(A_t\) eylemi ve \(R_t\) ödülü için;
\[H_{t+1}(A_t) = H_t(A_t) + \alpha(R_t - \overline{R_t})(1 - \pi_t(A_t)),a = A_t\] \[H_{t+1}(a) = H_t(a) - \alpha(R_t - \overline{R_t})\pi_t(a), \qquad \qquad \quad a \neq A_t\]\(\alpha > 0\) adım değeri için, \(\overline{R_t}\in\mathbb{R}\) şu ana kadar ve şu an dahil olmak üzere tüm ödüllerin ortalaması olacak şekilde hesaplanmaktadır. Eğer şu anki ödül, ortalamadan yüksekse; \(A_t\) eyleminin gelecekte seçilme olasılığı artmış olacak; düşük ise tam tersi olacaktır.
Ödüllerin normal dağılımına ortalama olarak \(+4\) eklenmiş hali, bazlı (with baseline) ve bazsız (without baseline) olarak Şekil \(2.5\)‘te gösterilmiştir. Baz (baseline) olmadan performans zayıflamaktadır.
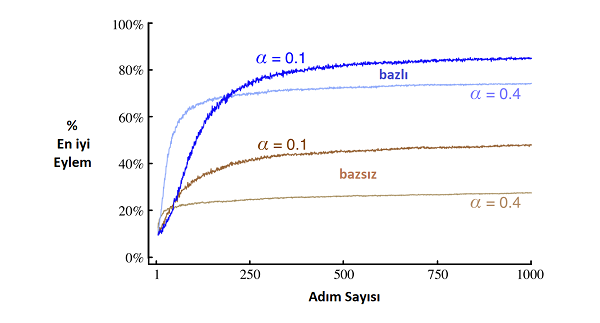\(\qquad\qquad\qquad\qquad\qquad\qquad\)Şekil 2.5 \(:\) Ödüllerin Dağılımı
İlişkili Arama (Bağlamsal Haydutlar)
Şimdiye kadar hep ilişkisiz (non-associative) görevlerden bahsedildi. Yani seçimlerin bir bağlama göre yapılmadığı problemlerdi. Problem durağan ise tek bir en iyi eylem vardı ve o eylem bulunmaya çalışılıyordu veya durağan değilse en iyi eylemin zamanla değişimini takip etmek gerekiyordu. Lâkin, gerçek Pekiştirmeli Öğrenme problemlerinde, o anki durumu gözlemleyip kararlar ona göre verilmektedir. Bu yüzden, gerçeğine daha yakın bir problem olarak kararların o anki duruma göre verildiği ilişkili arama veya bağlamsal haydutlar görülecektir.
Bağlamsal haydutları örneklemek için yine slot makinelerini verilebilir fakat bu sefer çok kollu tek bir makine yerine yine renk yahut isim gibi bağlamı verebilecek ayırt edici özelliklere sahip çok kollu birden fazla makine düşünülmelidir. Birden fazla makine olması sebebiyle her bir makinede en iyi ödül veren kol farklı olacaktır ve eylem kararı verilirken hangi makine için seçim yapıldığı bilinirse çok daha başarılı bir sonuç elde edilecektir. Bu örnekte durum (state) veya bağlam, seçim yapılacak makinede kullanılmaktadır.
Genel olarak haydut probleminin gerçek pekiştirmeli öğrenme problemlerinden eksik olan kısmı ise seçilen eylemin bir sonraki durumu etkilememesidir. Gerçek pekiştirmeli öğrenme probleminde ajan o anki durumu gözleyip buna göre bir eylem almaktadır. Bu eylemlerin sonucunda bu eyleme karşılık gelen ödülü alıp yeni bir duruma geçmektedir. Mevzubahis haydutlarda ise bir sonraki durum, alınan eylemlerden bağımsızdır. Yukarıdaki örnekte, seçilen kol aynı zamanda bundan sonra hangi makinenin geleceğini etkileseydi bu gerçeğe çok daha yakın bir problem olurdu. Aşağıdaki tabloya bakılırsa üç problemin farkları daha anlaşılır olacaktır.