Pekiştirmeli Öğrenme - Bölüm 8: Tabular Metotlar

Pekiştirmeli Öğrenme - Bölüm 8: Tabular Metotlar

Planlama ve Tabular Metotlar ile Öğrenme

Bu bölümde ortam modeli gerektiren ve model olmadan kullanılabilen pekiştirmeli öğrenme yöntemlerini göreceğiz. Bu iki yöntemin benzer ve farklı yanları vardır. En önemli farklılıkları; model gerektiren yöntemlerin temel bileşeni planlama iken model içermeyen yöntemlerin öğrenmeye dayalı bir temel bileşene sahip olmasıdır. En önemli benzerlikleri ise, değer fonksiyonlarının hesaplama gereksinimleridir. Bu bölümdeki amacımız model gerektiren ve model içermeyen yöntemlerin birleştirilmesidir (integration).

Modeller ve Planlama

Model, bir durum ve eylem verildiğinde, bir sonraki durum ve ödülün tahminini yapar. Eğer model stokastik ise durum ve ödül tahmini, birden çok sayıda ve olasılıklarıyla beraber hesaplanır. Dağıtım modeli (distribution model), bir probleme ait tüm olasılıkları ve açıklamaları üretir. Örnek olarak, \(p(s',r|s,a)\) bir dağıtım modelidir. Örnek model (sample model) ise, olasılıklara göre örneklenmiş yalnızca bir ihtimal için üretilir. Dağıtım modeli, örnek modele göre daha güçlü fakat her olasılığı ziyaret etme gereksinimi olduğu için hesaplaması çok daha zor ve zaman açısından dezavantajlıdır.Modelleri, deneyimi taklit etmek veya simüle etmek için kullanabiliriz. Bir başlangıç durumu ve eylemi aldığımızda örnek bir model, olası bir geçişi üretirken, bir dağıtım modeli, ortaya çıkma olasılıklarıyla birlikte tüm olası geçişleri de üretir. \begin{align} Model \rightarrow Taklit \ Deneyimi \rightarrow Değerler \rightarrow Politika
\end{align} Hem öğrenme hem de planlama yöntemlerinde en önemli durum, güncelleme işlemlerini yedekleyerek değer fonksiyonlarının tahmin edilmesidir. Planlamalı bir model, öğrenme yöntemi olarak çevre tarafından yaratılan gerçek deneyimi kullanmaktadır. Öğrenme yöntemleri deneyim gerektirir ve çoğu durumda gerçek deneyimin yanı sıra yapay olarak üretilmiş deneyimle de uygulanabilir.Aşağıdaki örneğimiz, \(Q\)-öğrenmeye ve rastgele örneklere dayanan bir planlama yöntemidir. Tabular \(Q\)-öğrenme de gerçek ortama en uygun politika, her durum ve aksiyon çiftinde sonsuz sayıda seçilebilir ve \(\alpha\) ise uygun olarak azalmalıdır.

Diğer konumuz ise küçük aşamalı adımlar halindeki planlamanın faydalarıdır. Bu durum, planlama ile modelin öğrenilmesi için gereklilikdir. Küçük aşamalı planlamalar, saf planlama problemlerinde en verimli planlama modeli olabilir.

Dyna: Entegre Planlama, Oyunculuk (Acting) ve Öğrenme

Etkileşimlerden elde edilen yeni bilgilerle model değişebilir ve planlama ile etkileşime girer. Karar verme ve model öğrenme hesaplamaları yoğun süreçler içerir, bu durumda mevcut hesaplama kaynaklarının aralarında bölünmesi gerekebilir. Bu konuları keşfetmeye başlamak için basit bir mimari olan Dyna-\(Q\)‘yu anlatacağız. Her işlev Dyna-\(Q\)‘da basit, neredeyse önemsiz bir biçimde görünür. Bir planlama ajanının içinde, gerçek deneyim için en az iki rol vardır: Birincisine model-öğrenme ve ikincisine ise doğrudan pekiştirmeli öğrenme (Direct RL) diyoruz. Deneyim, model, değerler ve politika arasındaki olası ilişkiler diyagramda aşağıda özetlenmiştir.

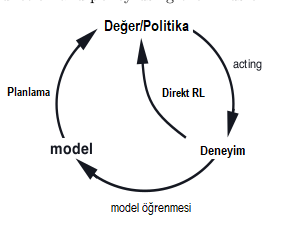
Hem doğrudan hem de dolaylı yöntemlerin avantaj ve dezavantajları vardır. Dolaylı yöntemler genellikle sınırlı bir deneyim miktarını daha fazla kullanır ve böylece daha az çevresel etkileşim ile daha iyi bir politikaya ulaşırlar. Doğrudan yöntemler daha basittir ve modelin tasarımında önyargılardan etkilenmez. Dyna-\(Q\), yukarıdaki şemada gösterilen tüm süreçleri içerir; planlama, oyunculuk(acting), model öğrenme ve doğrudan pekiştirmeli öğrenme. Planlama yöntemi, rastgele örneklemeli, tek adımlı tabular \(Q\) planlama yöntemidir. Doğrudan pekiştirmeli öğrenme yöntemi ise tek adımlı tabular \(Q\)-öğrenmedir. Model öğrenme metodu da tabana dayalıdır ve çevrenin deterministik olduğunu varsayar. Her geçişten sonra \(S_t\), \(A_t \rightarrow R_{t+1}\), \(S_{t+1}\), modelin, \(S_t\) için tablo girişinde kaydedilmesi, \(R_{t+1}, S_{t+1}\)‘in deterministik olarak izleyeceği tahminidir. Bu nedenle, model daha önce deneyimlenen durum eylemi çifti ile sorgulandığında, sadece son gözlemlenen durumu ve bir sonraki ödülün öngörüsü olarak döngüye devam eder. Dyna ajanlarının genel mimarisi aşağıda yer almaktadır. Bu mimariyi anlamak oldukça önemlidir model yapımızın genel bir özeti gibi aslında. Merkez sütun, aktör ve çevre arasındaki temel etkileşimi temsil eder ve gerçek deneyimin bir yörüngesine yol açar. Figürün solundaki ok, değer fonksiyonunu ve politikayı geliştirmek için gerçek deneyim üzerinde çalışan doğrudan takviye öğrenimini temsil ederken, sağda da model tabanlı süreçleri vardır. Model, gerçek deneyimler ile öğrenir ve simüle etmek deneyime yol açar. Dönem arama kontrolünü, modelin oluşturduğu simüle edilmiş deneyimler için başlangıç durumlarını ve eylemleri seçen süreci anlatmak için kullanırız. Dyna-\(Q\)‘da olduğu gibi, aynı güçlendirme öğrenme metodu hem gerçek deneyimlerden hem de simüle edilmiş deneyimlerin planlaması için kullanılır. Güçlendirme öğrenme yöntemi, hem öğrenme hem de planlama için “nihai ortak yol” dur. Öğrenme ve planlama, hemen hemen tüm makineyi paylaşma anlamında derinden bir bütünleşmesi söz konusudur, sadece deneyimlerinin kaynağında farklılıklar gösterir.

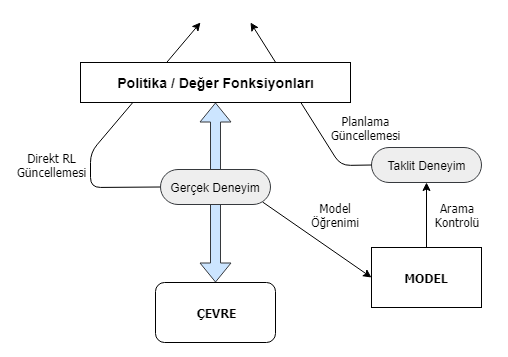
Şekil 8.1 : Genel Dyna Mimarisi. Çevre ve politika arasında gidip gelen gerçek deneyim, politika ve değer işlevlerini, çevre modeli tarafından üretilen simüle edilmiş deneyimle aynı şekilde etkiler.

Kavramsal olarak planlama, oyunculuk, model-öğrenme ve doğrudan pekiştirmeli öğrenme , Dyna ajanlarında aynı anda ve paralel olarak meydana gelir. Dyna-\(Q\)‘da oyunculuk, model-öğrenme ve doğrudan pekiştirmeli öğrenme süreçleri çok az hesaplama gerektirir.

Örneğin, Şekil 8.2’de gösterilen basit labirent örneğini düşününelim. 47 durumun her birinde, hareketin bir engel veya labirentin kenarı tarafından engellendiği durumlar hariç, ilgili komşu durumları deterministik olarak ajanı götüren yukarı, aşağı, sağa ve sola doğru dört eylem vardır. Ödül, +1 olduğu hedef durumdakiler hariç, tüm geçişlerde sıfırdır. Hedef durumuna (G) ulaştıktan sonra, ajanı yeni bir bölüme başlamak için başlangıç durumuna (S) geri döner. Bu, \(γ\) = 0,95 ile indirimli, epizodik bir görevdir.

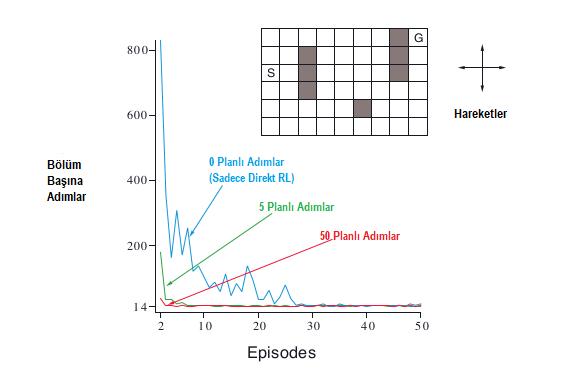
Şekil 8.2 : Basit labirent (üst metin) ve gerçek adım başına planlama adımı (n) sayılarında değişen Dyna-\(Q\) aracıları için ortalama öğrenme eğrileri. Amaç (S)’den (G)’ye en kısa yoldan ulaşmaktır.

Dyna-\(Q\) ajanlarının labirent görevine uygulandığı bir deneyden ortalama öğrenme eğrilerini göstermektedir. Başlangıçtaki eylem değerleri sıfırdır, adım büyüklüğü parametresi \(\alpha = 0.1\) ve keşif parametresi \(\varepsilon = 0.1\)’ dir. Eylemler arasında açgözlü(greedly) seçerken, bağlar rastgele kırılır. Ajanların, planlama adımlarının sayısı da değişir. Her bir \(n\) için eğriler, ajanın her bölümdeki hedefe ulaşmak için attığı adımlarının sayısını gösterir.İlk bölüm, tüm \(n\) değerleri için tam olarak aynıydı (yaklaşık 1700 adım) ve verileri şekilde gösterilmiyor. Parametre değerleri (\(\alpha\) ve \(\varepsilon\)) bunun için optimize edilmiş olmasına rağmen, bu problemin en yavaş maddesiydi. Planlanmayan ajan, (\(\varepsilon\)-) optimal performansa ulaşmak için yaklaşık \(25\) bölüm alırken, \(n = 5\) ajanı yaklaşık beş bölüm aldı ve \(n = 50\) ajanı sadece üç bölüm aldı.

Şekil 8.3, planlama ajanlarının çözümlemeyi neden plansız ajandan çok daha hızlı bulduğunu göstermektedir. Gösterilenler, ikinci bölümün ortasında \(n = 0\) ve \(n = 50\) aracı tarafından bulunan politikalardır. Planlama olmadan (\(n = 0\)), her bölüm politikaya yalnızca bir ek adım daha ekler ve bu nedenle şimdiye kadar sadece bir adım öğrenildi. İkinci bölümde, ajanı başlangıç durumuna yakın bir yerde dolaşırken, planlama süreci tarafından oluşturulmuştur. Üçüncü bölümün sonunda tam bir optimal politika bulunacak ve mükemmel performans elde edilecek.

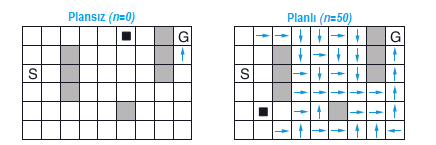
Şekil 8.3 : İkinci bölümün yarısında Dyna-\(Q\) ajanlarının planlanması ve planlamaması ile bulunan politikalar. Siyah kare ajanın yerini gösterir.

Dyna-\(Q\)‘da öğrenme ve planlama tam olarak aynı algoritma ile gerçekleştirilir, öğrenme için gerçek deneyime ve simüle edilmiş deneyime dayalı olarak çalışır. Her ikisi de olabildiğince hızlı ilerler. Ajan her zaman reaktiftir ve daima müzakereci olur, en son duyusal bilgilere anında cevap verir ve her zaman arka planda plan yapar. Ayrıca arka planda devam eden model öğrenme sürecidir. Yeni bilgiler elde edildiğinde, model gerçeğe daha iyi uyum sağlamak için güncellenir. Model değiştikçe, devam eden planlama süreci yavaş yavaş yeni modeli eşleştirmek için davranış tarzı sergiler.

Model Yanlış Olduğunda

Boş olarak başlayan model ve sonrasında sadece doğru bilgilerle doldurulur desek de genel olarak bu kadar şanslı olmayı beklemeyiz. Ortam stokastiktir ve sadece sınırlı sayıda örnek ile gözlemlenmektedir. Bu yüzden model yanlış olabilir. Model yanlış demek; kusurlu şekilde genelleştiren fonksiyon yaklaşımı kullanılması ya da çevrenin değiştiği için yeni davranışın henüz gözlemlenmediği öğrenilmiştir. Model yanlış olduğunda planlanma sürecinin optimal bir politika oluşturması muhtemeldir.

Bazı durumlarda, planlama ile hesaplanan optimal politika hızlı bir şekilde modelleme hatasının keşfine ve düzeltilmesine yol açar. Bu, modelin gerçekte mümkün olandan daha iyi ödül veya daha iyi durum geçişleri öngörme anlamında iyimser olduğu zaman gerçekleşme eğilimindedir. Planlanan politika bu fırsatları istismar etmeye çalışır.

Örneğin, başlangıçta şeklin sol üst köşesinde gösterildiği gibi, başlangıçtan kaleye, bariyerin sağına doğru kısa bir yol vardır. 1000 zaman adımından sonra, kısa yol “bloke edilir” ve şeklin sağ üst köşesinde gösterildiği gibi bariyerin sol tarafı boyunca daha uzun bir yol açılır. Grafik, bir Dyna-\(Q\) ajanı ve geliştirilmiş Dyna-\(Q\) + maddesinin kısa bir süre için açıklanması için ortalama kümülatif ödül göstermektedir. Grafiğin ilk kısmı, Dyna ajanlarının her iki adımda 1000 adımda kısa yol bulduğunu göstermektedir. Ortam değiştiğinde, grafikler düzleşerek, ajanların ödüllendirilmediği bir dönemi belirtiyorlar, bariyerin arkasında dolaşıyorlardı. Ancak bir süre sonra yeni açılımı ve yeni optimal davranışı bulabiliyorlar.

Çevrenin daha öncekinden daha iyi hale gelmesiyle birlikte daha büyük zorluklar ortaya çıkar, ancak eskiden beri doğru olan politika iyileştirmeyi ortaya çıkarmıyor. Bu durumlarda modelleme hatası uzun bir süre için tespit edilemez.

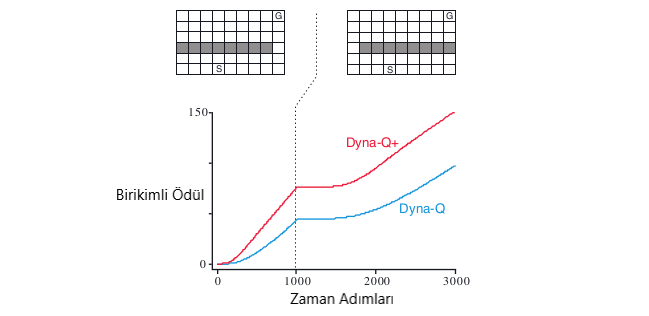
Şekil 8.4 : Bir engelleme görevinde Dyna ajanlarının ortalama performansı. Sol çevre ilk 1000 adım için, geri kalanı için doğru ortam olarak kullanılmıştır.Dyna-\(Q\)+, keşfi teşvik eden bir keşif bonusu olan Dyna-\(Q\)‘dur.

Diğer örneğimizde ise, öncelikle en uygun yol bariyerin sol tarafına gitmek (Şekil 8.4). Ancak, 3000 adımdan sonra, sağ taraf boyunca daha kısa bir yol açılır. Grafik, normal Dyna-\(Q\) ajanının hiçbir zaman kısayola geçmediğini göstermektedir. Onun modeli hiçbir kısayol olmadığını, bu yüzden ne kadar planladığını, sağa doğru adım atmanın ve onu keşfetmenin daha az muhtemel olduğunu görüyoruz. \(\epsilon-\)açgözlü (greedy) bir politikada bile, bir ajanın kısayolu keşfetmek için pek çok keşif eylemi gerçekleştirmesi pek olası değildir.

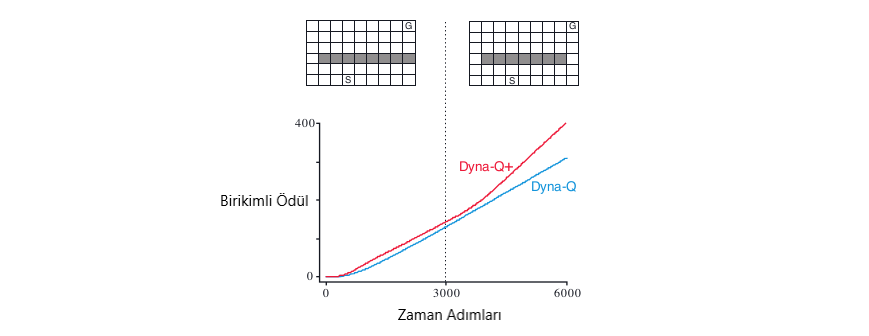
Şekil 8.5 : Bir kısayol görevinde Dyna aracılarının ortalama performansı.

Buradaki genel sorun, keşif ve sömürü arasındaki çatışmanın başka bir versiyonudur. Bir planlama bağlamında keşif, modeli geliştiren eylemleri denemek anlamına gelirken, mevcut model dikkate alındığında, sömürü en uygun davranış anlamına gelir. Ajanın çevrede değişiklikler bulmak için keşfe çıkmasını istiyoruz, ancak performansının aşırı düşmesi durumuna kadar değil. Daha önceki keşif / sömürü çatışmasında olduğu gibi, muhtemelen hem mükemmel hem de pratik bir çözüm yoktur, ancak basit sezgisel yöntemler genellikle etkilidir.

Kısayol labirentini çözen Dyna-\(Q\) + aracı, bu tür planlamalarda kullanılır. Bu ajanı, çiftin en son çevre ile gerçek bir etkileşim içinde denenmesinden bu yana kaç zaman adımının geçtiğine ilişkin her bir durum eylem çiftini izler. Daha fazla zaman geçtikçe, bu çiftin dinamiklerinin değiştiğini ve bu modelin yanlış olduğunu daha iyi tahmin edebiliriz. Uzun süreli olmayan eylemleri test eden davranışları teşvik etmek için, bu eylemleri içeren simüle edilmiş deneyimlere özel bir “bonus ödülü” verilir. Özellikle, bir geçiş için modellenmiş ödül \(r\) ise ve geçiş \(τ\) zaman adımlarında denenmemişse, bu geçişin bir \(r + κ √ τ\) ödülü ürettiği gibi yapılır. Bu, ajanı tüm erişilebilir durum geçişlerini test etmeye ve hatta bu tür testleri gerçekleştirebilmek için uzun eylem dizileri bulmaya teşvik eder. Elbette tüm bu testlerin maliyeti vardır, fakat çoğu durumda, kısayol labirentinde olduğu gibi, bu tür bir hesaplama merakı da ekstra keşif yapmaya değerdir.

Öncelikli Süpürme

Önceki bölümlerde sunulan Dyna ajanlarında, simüle edilmiş geçişler, daha önce deneyimlenen tüm çiftlerden rastgele olarak seçilen durum-eylem çiftlerinde başlatılmaktadır. Ancak tek tip bir seçim genellikle en iyisi değildir; simüle edilmiş geçişler ve güncellemeler belirli durum-eylem çiftlerine odaklanırsa planlama çok daha verimli olabilir. İkinci bölümün başlangıcında, doğrudan hedefe giden durum eylem çiftinin olumlu bir değeri vardır; diğer tüm çiftlerin değerleri hala sıfırdır. Bu, hemen hemen tüm geçişler boyunca güncellemeleri gerçekleştirmenin anlamsız olduğu anlamına gelir, çünkü ajanı sıfır değerli bir durumdan diğerine taşırlar ve bu nedenle güncellemelerin hiçbir etkisi olmaz. Sadece hedeften hemen önce ya da ondan sonraki bir durum boyunca olan güncelleme herhangi bir değeri değiştirecektir. Eğer simüle edilmiş geçişler tekdüze olarak üretilirse, bu yararlı olanlardan birine gelmeden önce çok sayıda savurgan(wasteful) güncelleme yapılacaktır. Planlama ilerledikçe, yararlı güncellemeler bölgesi büyür, ancak planlama, en iyi işi yapacaksa odaklanmış olmasından dolayı çok daha az verimlidir. Gerçek hedefimiz olan daha büyük sorunlarda, durumların sayısı o kadar büyük ki, odaklanmamış bir aramanın aşırı derecede verimsiz olacağını görmekteyiz.

Bu örnek, aramanın hedef durumlardan geriye doğru çalışarak yararlı bir şekilde odaklanabileceğini göstermektedir. Daha çok genel ödül fonksiyonları için çalışan yöntemler istiyoruz. Genel olarak, sadece hedef durumlardan değil, değerinin değiştiği herhangi bir durumdan da geri dönmek istiyoruz. Hedefi keşfetmeden önce labirent örneğinde olduğu gibi, değerlerin modele göre ilk başta doğru olduğunu varsayarsak, şu anda ajanın çevrede bir değişiklik keşfettiğini ve yukarı ya da aşağı bir tahmin edilen bir durum değerini değiştirdiğini varsayalım. Tipik olarak, diğer birçok durumun değerinin değiştirilmesi gerektiği anlamını taşır. Ancak yararlı olacak tek adım güncellemeleri, değeri değiştirilmiş olan yalnız bir duruma yönlendiren eylemlerdir. Bu eylemlerin değerleri güncellenirse, önceki durumların değeri de sırayla değişebilir olacaktır. Öyleyse, bunları yönlendiren işlemlerin güncellenmesi gerekmektedir ve böylece önceki durumlar da değişmiş olur. Böylelikle, değerli güncellemeler gerçekleştirerek ya da yayılımı sona erdirerek, değeri değişmiş olan keyfi durumlardan geriye doğru çalışabilir. Bu genel fikir, planlama hesaplamalarının geriye doğru odaklanması olarak adlandırılabiliriz.

Yararlı güncellemelerin sınırı geriye doğru yayılırken, çoğu zaman hızla büyüyerek, yararlı bir şekilde güncellenebilecek pek çok durum-eylem çiftini üretmektedir. Ancak bunların hepsi eşit derecede yararlı olmayacaktır. Güncellemeleri aciliyetlerinin bir ölçüsüne göre önceliklendirmek ve bunları öncelik sırasına göre gerçekleştirmek doğaldır. Öncelikli süpürme ardındaki fikir budur. Tahmin edilen değerin, değiştiğinde, öncelik büyüklüğüne göre önceliklendirildiği takdirde, tahmini değeri değişmeyecek olan her durum eylemi çiftinden bir sıra korunur. Kuyruktaki üst çift güncellendiğinde, önceki çiftlerinin her biri üzerindeki etki hesaplanır. Etki, küçük eşikten daha büyük olması durumunda (sıraya çiftinde bir önceki giriş olup olmadığını, kuyrukta kalan sadece yüksek öncelikli girdi daha sonra ekleme sonuçları), daha sonra bir çift yeni öncelikli sıraya sokulur. Bu şekilde değişikliklerin etkileri, etkili olana kadar geriye doğru yayılır.

Bu bölümde, tüm durumların alan planlaması yalnızca güncellemenin türü, büyük ya da küçük güncellemelerin yapıldığı sıraya göre değişen değer dizileri olarak görülemeyeceğinin önermesini inceledik. Bu bölümde geri odaklanma vurgulandı, ama bu sadece bir stratejidir. Örneğin, bir diğeri, mevcut politikada sıkça ziyaret edilen durumların ne kadar kolay ulaşılabileceğine, yani ileri odaklama olarak tanımlayacağımız duruma göre odaklanmak olacaktır (Peng ve Williams (1993) ve Barto, Bradtke ve Singh (1995) ileri odaklama çalışmalarını araştırmışlardır ve sonraki birkaç bölümde ortaya konan yöntemleri düzenlemişlerdir.).

Beklenen ve Örnek Güncellemeler

Bu iki boyut, \(q_{*},\) \(v_{*},\) \(q_{\pi}\) ve \(v_{\pi}\) olmak üzere dört değer fonksiyonuna yaklaşmak için dört güncellemeye yol açar. İki boyutlu aşağıda gördüğümüz gibi, yedi tanesi spesifik algoritmalara karşılık gelen sekiz olaya yol açar (Sekizinci olay herhangi bir yararlı güncellemeye karşılık gelmiyor). Bu tek adımlı güncellemelerin herhangi biri planlama yöntemlerinde kullanılabilir. Daha önce tartıştığımız Dyna-\(Q\) ajanları \(q_{*}\) örnek güncellemelerini kullanmaktadır. Dyna-AC sistemi, bir öğrenme politikası yapısıyla birlikte \(v_{\pi}\) örnek güncellemeleri kullanır. Stokastik problemler de öncelikli süpürme her zaman yapılan güncellemelerden biri kullanılarak yapılır.

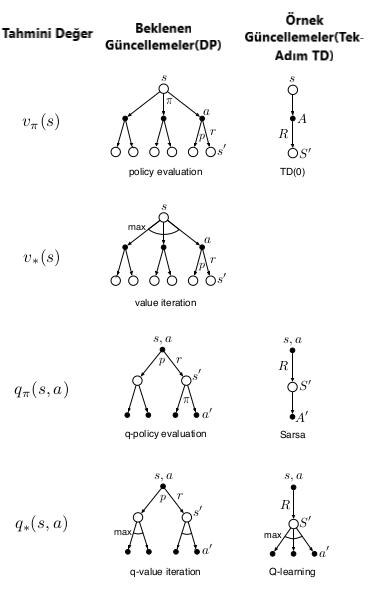
Şekil 8.6 : Bu kitapta ele alınan tüm tek adımlı güncellemeler için yedekleme diyagramları.

Bir dağıtım modelinin yokluğunda, beklenen güncellemeler mümkün değildir, ancak örnek güncellemeleri çevre veya örnek bir modelden örnek geçişleri kullanılarak yapılabilir. Bu bakış açısında mümkünse eğer, beklenen güncellemelerin tercih edilmesidir. Beklenen güncellemeler, örnekleme hatasından dolayı bozulmadığı için daha iyi bir tahminde bulunacaktır, ancak aynı zamanda daha fazla hesaplama gerektirir ve hesaplama genellikle planlamada sınırlayıcı bir kaynaktır. Planlama için beklenen ve örnek güncellemeleri değerlendirebilmek için farklı hesaplama gereksinimlerini kontrol etmeliyiz. Yaklaşık değer fonksiyonu, \(Q\) ve tahmini dinamikler şeklinde bir model ile gösterecek olursak, \(p(s',r|s,a)\) şeklindedir. Bir durum eylem çifti için beklenen güncelleme ise, \(s,a :\)

\[Q(s,a) \gets \sum\limits_{s',r}\big[r + \gamma \max\limits_{a'} Q(s',a') \big] \qquad (8.1)\]

Bir sonraki durum ve ödül, \(S^{'}\) ve \(R\) modelinden örnek verirsek \(s, a\) için örnek güncellemesi,

\[Q(s,a) \gets Q(s,a) + \alpha \bigg[R + \gamma Q(S', a') - Q(s,a)\bigg] \qquad (8.2)\]

burada \(\alpha\), olağan pozitif adım büyüklüğü parametresidir. Bu beklenen ve örnek güncellemeleri arasındaki fark, ortamın stokastik olduğu ölçüde, özellikle de, bir durum ve eylem verildiğinde, bir çok olası durumun çeşitli olasılıklarla ortaya çıkabileceği ölçüde önemlidir. Eğer bir sonraki durum mümkün ise, yukarıda verilen beklenen ve örnek güncellemeleri aynıdır (\(\alpha = 1\) alarak). Beklenen güncellemenin lehine, kesin bir hesaplama olması ve doğruluk durumlarının yalnızca \(Q(s,a)\)‘nın ardışıl durumlarındaki doğruluğu ile sınırlanan yeni bir \(Q(s,a)\) ile sonuçlanmasıdır. Örnek güncelleme ayrıca örnekleme hatasından etkilenir. Öte yandan, örnek güncelleme daha hesaplı bir şekilde daha ucuzdur, çünkü tüm olası durumları değil, yalnızca bir sonraki durumu dikkate alır. Uygulamada, güncelleme işlemlerinin gerektirdiği hesaplama genellikle \(Q\)‘nun değerlendirildiği durum-eylem çiftlerinin sayısına göre belirlenir. Belirli bir başlangıç çifti için, \(s,a\), dallanma faktörü (yani, sonraki muhtemel durumların sayısı, \(s,p\) için \((s_0|s,a)>0\) olsun. Daha sonra bu çiftin beklenen bir güncellemesi, örnek güncelleme olarak kabaca b katı kadar hesaplama gerektirir. Beklenen bir güncellemeyi tamamlamak için yeterli süre varsa, sonuçta elde edilen tahmin, örnekleme hatasının olmaması nedeniyle, \(b\) örnek güncellemelerinden genellikle daha iyidir. Ancak, beklenen bir güncellemeyi tamamlamak için yeterli süre yoksa, örnek güncellemeleri her zaman tercih edilir çünkü bunlar en az b güncellemelerinden daha düşük bir değere sahip bir değer artışı yapar. Birçok durum eylemi çiftiyle ilgili büyük bir problemde, genellikle ikinci durumumuz mevcuttur. Çok sayıda durum eylemi çifti ile, hepsinin beklenen güncellemeleri çok uzun zaman alacaktır. Bundan önce, birkaç durumda güncellemeyle, çiftlerde beklenen güncellemelere kıyasla çok daha iyi olabiliriz. Bir dizi hesaplama çabası göz önüne alındığında, birkaç beklenen güncellemeye veya \(b\) defa tekrarlanan birçok örnek güncellemeye ayrılmalı mı?

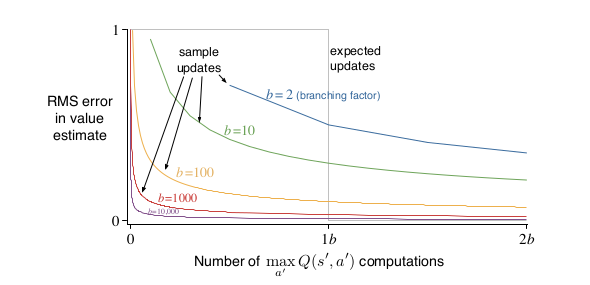
Şekil 8.7 : Beklenen ve örnek güncellemelerin verimliliğinin karşılaştırılması.

Şekil 8.7, bu sorunun cevabını öneren bir analizin sonuçlarını göstermektedir. Tahmin etme hatasını çeşitli dallanma faktörleri için beklenen ve örnek güncellemeleri için hesaplama zamanının bir fonksiyonu olarak gösterir, \(b\) göz önünde bulundurulması gereken durum, tüm \(b\) halefi durumların eşit derecede muhtemel olduğu ve ilk tahmindeki hatanın 1 olduğu durumdur. Bir sonraki durumlardaki değerler doğru olarak kabul edilir, dolayısıyla beklenen güncelleme hatayı tamamlandığında sıfır \(q\)‘ya indirir. Bu durumda, örnek güncellemeler, \(= \sqrt\frac{b-1}{bt}\) ‘ye göre hatayı azaltmaktadır, burada t, gerçekleştirilen örnek güncellemelerinin sayısıdır (örnek ortalamalarının varsayılması, yani \(a=1/t\)). Bu durumlar için, bir çok durum-eylem çiftinin değerleri, beklenen bir güncellemenin etkisinin yüzdesi içinde, önemli ölçüde iyileştirilmiş olabilir, aynı zamanda, tek bir durum-eylem çiftinin beklenen bir güncellemeden geçmesi de mümkündür.

Şekil 8.7’de gösterilen örnek güncellemelerin avantajı, gerçek etkinin bir tahminidir. Gerçek bir problemde, varis(successor) durumların değerleri, kendilerinin güncellenmiş tahminleri olacaktır. Örnek güncellemelerin ikinci bir avantajı, ardışıl durumlardan yedeklenen değerlerin daha doğru olacağıdır. Bu sonuçlar, örnek güncellemelerin büyük stokastik dallanma faktörleri ve tam olarak çözülecek çok fazla durum ile ilgili sorunlarda beklenen güncellemelere kıyasla daha üstün olduğunu göstermektedir.

Yörünge Örneklemesi

Dinamik programlamada klasik yaklaşım, tüm durum alanı boyunca birer birer güncelleme yaparak, tüm durum alanı boyunca tarama yapmaktır. Bu büyük görevlerde problemlidir çünkü bir silme işlemini tamamlamak için zaman olmayabilir. Kapsamlı taramalar, ihtiyaç duyulan ilgili yere odaklanmak yerine, durum uzayının tüm bölümlerine eşit zaman ayırır. Kapsamlı taramalar ve ifade ettikleri bütün durumların eşit davranışı, dinamik programlamanın gerekli özellikleri değildir. Prensip olarak, güncellemeler herhangi bir şekilde dağıtılabilir.

Dyna-\(Q\) ajanında olduğu gibi tekdüze bir örnek alınabilir, ancak bu kapsamlı taramalar ile aynı sorunlardan bazılarına maruz kalacaktır. Daha cazip olanı ise güncellemeleri politikaya göre dağıtmaktır. Bu dağıtımın bir avantajı, kolayca üretilebilmesidir; mevcut politikadan sonra model ile etkileşime girer. Devam eden bir görevde her yerde başlar ve simüle etmeye devam eder. Her iki durumda da örnek durum geçişleri ve ödülleri model tarafından verilir ve örnek eylemler mevcut politika tarafından verilir. Biz deneyim üretme yolunu ararız ve yörünge örneklemesini güncelleriz.

Eğer bir kişi, politika-içi dağıtımın açık şekilde sahip olsaydı, politika-içi dağıtıma göre güncellemeyi ağırlıklandırarak, tüm durumları kapsayabilirdi. Politika dışı dağıtımın açık bir biçimde bilinmesi bile olası değildir. Dağıtım, politika değiştiğinde ve dağıtımın hesaplanması, tam bir politika değerlendirmesine eşdeğer bir hesaplamayı gerektirdiğinde değişir. Bu gibi diğer olasılıkların göz önünde bulundurulması, yörünge örneklemesinin hem verimli hem de zarif görünmesini sağlar.

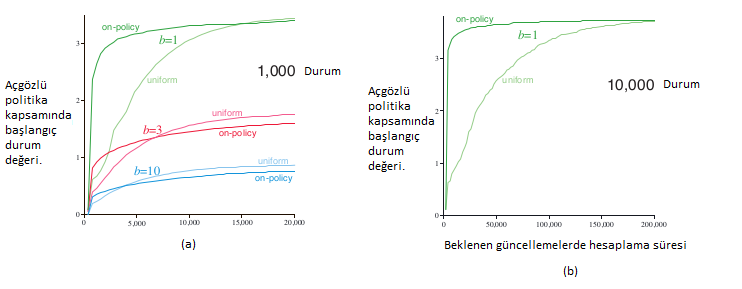
Şekil 8.8 : Her biri aynı durumda başlayan, simüle edilmiş politika üzerinde yörüngelere odaklanmak yerine, durumun tamamında eşit olarak dağıtılan güncellemelerin göreceli etkinliği.

Şekil-8a, 1000 durum ile 1, 3 ve 10’luk dallanma faktörleriyle ortalama olarak 200’den fazla örnek görevi göstermektedir. Etkisi daha güçlü ve daha küçük dallanma faktörlerinde daha hızlı planlamanın ilk periyodu daha uzundur. Diğer deneylerde, bu etkilerin zamanla sayısı arttıkça daha da güçlendiğini gördük. Örneğin, Şekil-8b kısmı 10,000 durumlu görevler için 1’lik bir dallanma faktörü için sonuçları gösteriyor. Bu durumda, politika odaklı olmanın avantajı geniş ve uzun ömürlü olmasıdır. Politikanın dağılımına göre örnekleme, başlangıç durumlarına yakın olan durumlara odaklanarak yardımcı olmaktır. Uzun vade de, politikadaki dağıtıma odaklanmak zarar verebilir.

Gerçek Zamanlı Dinamik Programlama

Gerçek zamanlı dinamik programlama değer yineleme algoritmasının bir politika-yörünge-örnekleme sürümüdür. Geleneksel süpürme temelli politika iterasyonu ile yakından ilişkilidir. Gerçek zamanlı dinamik programlama, gerçek veya simüle edilmiş yörüngelere ziyaret edilen durumların değerlerini, değer yineleme güncellemeleri aracılığıyla günceller. Temel olarak Şekil 8.8 de gösterilen politika üzerinde sonuçları üreten algoritmadır.

Gerçek zamanlı dinamik programlama ve konvansiyonel dinamik programlama arasındaki yakın bağlantı, mevcut teoriye uyarlayarak bazı teorik sonuçların elde edilmesini mümkün kılmaktadır. Gerçek zamanlı dinamik programlama, asenkron dinamik programlama algoritmasının bir örneğidir. Eş zamansız dinamik proglama algoritmaları, durum setinin sistematik taraması açısından organize edilmez, diğer eyaletlerin değerleri ne olursa olsun, herhangi bir sırayla durum değerlerini günceller. Gerçek zamanlı dinamik programlama da, güncelleme sırası, gerçek veya simüle edilmiş yörüngelere göre durumlar belirlenir.

Belirli bir politika için tahmin problemiyle ilgileniyorsak, politika-içi yörünge örneklemesi, algoritmanın ulaşılamayacak durumlarının tamamen atlamasına izin verir. Hedefin, belirli bir politikayı değerlendirmek yerine optimal bir politika bulmak için bir kontrol problemini ulaşılamayacak durumları olabilir.

Gerçek zamanlı dinamik programlamanın en ilginç sonucu, makul koşulları sağlayan belirli problemler için, optimal bir politika bulmayı garanti etmesidir. Bazı problemlerde, durumların sadece küçük bir kısmının ziyaret edilmesi gerekmektedir. Bu durumda, tek bir süpürmenin bile mümkün olmadığı çok büyük durum kümeleriyle ilgili problemler için büyük bir avantaj olabilir. Bu sonucun tutulduğu görevler, sıfır ödül üreten hedef durumları absorbe eden Markov Karar Problemleri için tekrar edilmeyen bölüm görevleridir. Gerçek veya simüle edilmiş bir yörüngenin her adımında, gerçek zamanlı dinamik programlama açgözlü bir eylemi seçer ve beklenen değer güncelleme işlemini mevcut duruma uygular. Ayrıca, her adımda diğer durumların değerlerini güncelleyebilir.

Bu sorunlar da tüm durumlar, en uygun politikaya yaklaşır:

1) Başlangıç değerinin her amaç durumu sıfırdır.

2) Herhangi bir başlangıç durumundan olasılıklarla hedefe ulaşılacağını garanti eden en az bir politika vardır.

3) Hedef olmayan durumlardan geçişler için tüm ödüller kesinlikle olumsuzdur.

4) Başlangıç değerleri, optimal değerlere eşit veya daha büyüktür.

Bu özelliklere sahip olan görevler, ödül maksimizasyonu yerine, genellikle maliyet minimizasyonu olarak ifade edilen stokastik optimal yol problemlerinin örnekleridir. Sürümümüzdeki negatif getirileri en üst düzeye çıkarmak, başlangıç durumundan hedef duruma giden yolların maliyetlerini en aza indirgemeye eşdeğerdir.

Karar Zamanında Planlama

Planlama en az iki yolla kullanılabilir. Dinamik programlama ve Dyna tarafından türetilen bölüm, bir modelden (örnek veya dağıtım modeli) elde edilen simüle edilmiş deneyime dayanarak bir politika veya değer fonksiyonunu kademeli olarak geliştirmek için bir planlama kullanılmaktadır.

Planlamayı kullanmanın diğer bir yolu, her yeni durum ile karşılaştıktan sonra, çıktısı tek bir eylemin seçimi olan bir hesaplama olarak başlamak ve tamamlamaktır. Planlamanın ilk kullanımından farklı olarak, planlama burada belirli bir duruma odaklanır, bu yüzden karar-zaman planlaması diyoruz.

Planlamayla ilgili iki yol vardır; bir politikayı veya değer işlevini zamanla iyileştirmek için simüle edilmiş deneyimleri kullanmak ya da mevcut durum için bir eylem seçmek için simüle edilmiş bir deneyim kullanımı şeklinde tanımlanabilir, ancak bunlar ayrı ayrı incelenmeye eğilimlidir.

Değerler ve politika mevcut duruma ve eylem seçimlerine özgüdür, mevcut eylemi seçmek için kullanıldıktan sonra planlama sürecinin oluşturduğu değerler ve politikalar tipik olarak atılır. Genel olarak, mevcut durum üzerine odak planlaması yapmak ve planlama sonuçları saklanmalı sonra da aynı duruma dönmelidir. Karar verme zamanı planlaması, hızlı yanıtların gerekli olmadığı uygulamalarda en kullanışlıdır. Örneğin, satranç oynama programlarında, her bir hareket için bir saniyelik veya dakika hesaplamaya izin verilebilir ve güçlü programlar bu süre içerisinde onlarca hamle planlayabilir. Öte yandan, düşük gecikme eylemi seçimi öncelikliyse, genel olarak her yeni karşılaşılan duruma hızla uygulanabilecek bir ilkeyi hesaplamak için arka planda planlama yapmak genellikle daha iyidir.

Sezgisel Arama

Sezgisel aramada, karşılaşılan her bir durum için, muhtemel sürekliliklerin için büyük bir ağaç düşünülür. Yaklaşık değer fonksiyonu, yaprak düğümlerine uygulanır ve daha sonra kökte mevcut duruma doğru yedeklenir. Yedekleme, mevcut durum için durum-eylem düğümlerinde durur. Bu düğümlerin yedeklenen değerleri hesaplandıktan sonra, bunların en iyisi geçerli eylem olarak seçilir ve sonra tüm yedek değerler atılır. Konvansiyonel sezgisel aramada, yaklaşık değer fonksiyonunu değiştirerek yedeklenen değerleri kaydetmek için uğraşılmaz. Açgözlü, \(\epsilon\)-açgözlü ve üst güven bağılı (UCB) eylem seçim yöntemleri, daha küçük ölçekli de olsa, keşifsel aramadan farklı değildir. Örneğin, bir model ve bir durum-değer fonksiyonu verilen açgözlü eylemi hesaplamak için, her bir olası eylemden önce her bir sonraki duruma dikkat etmeli, ödülleri ve tahmini değerleri hesaba katmalı ve en iyi eylemi seçmeliyiz. Geleneksel sezgisel aramada olduğu gibi, bu süreç olası eylemlerin yedeklenmiş değerlerini hesaplar, ancak bunları kaydetmeye çalışmaz. Sezgisel arama, açgözlü politika fikrinin bir adım ötesi olarak görülebilir.

Eğer arama, \(\gamma^{k}\) çok küçük olacak şekilde yeterli derinlikte ise, o zaman eylemler buna uygun olarak optimal olacaktır. Diğer yandan, arama ne kadar derin olursa, genellikle daha yavaş cevap süresi olur. Tesauro, sezgisel aramanın daha derin olduğunu, TD-ammon tarafından yapılan hamlelerin ne kadar iyi olduğunu, ancak her bir hamlenin süresinin ne kadar uzun sürdüğünü buldu. Tavla büyük bir dallanma faktörüne sahiptir, ancak hamleler birkaç saniye içinde yapılmalıdır. Seçmeli olarak birkaç adım ileriye doğru arama yapmak mümkün olabiliyor ancak arama bile önemli ölçüde daha iyi eylem seçimleriyle sonuçlanabilir.

Sezgisel aramanın, arama ağacının durumlara sıkı sıkıya odaklanması ve mevcut durumu hemen takip edebilecek eylemlerden kaynaklanmaktadır. Eylemleri nasıl seçerseniz seçin, güncellemeler için en yüksek önceliğe sahip olan ve yaklaşık değer işlevinizin en doğru şekilde, nerede olmasını istediğiniz bu durumlar ve eylemlerdir. Sadece hesaplamalarımızı yakın olaylara ayırmalı, aynı zamanda sınırlı bellek kaynağımız olmalıdır. Örneğin, satrançta, her bir hamle için ayrı değer tahminleri olduğundan çok fazla olası pozisyon vardır, ancak sezgisel aramaya dayalı satranç programları, karşılaştıkları milyonlarca konum için, tek bir konumdan ileriye dönük olarak karşılaşabilecekleri farklı tahminleri kolayca depolayabilirler.

Güncellemelerin dağıtımı, mevcut duruma ve olası haleflerine odaklanmak için benzer yollarla değiştirilebilir. Sınırlayıcı bir vaka olarak, bir arama ağacı inşa etmek için sezgisel arama yöntemlerini tam olarak kullanabilir ve Şekil 8.9’un önerdiği gibi tek tek, yukarıdan aşağı güncellemeleri gerçekleştirebiliriz. Güncellemeler bu şekilde sıralanırsa ve bir tablo temsili kullanılırsa, derinlik buluşsal aramada olduğu gibi tam olarak aynı genel güncelleme elde edilir. Herhangi bir durum alanı araştırması, bu şekilde çok sayıda tek adımlı güncellemenin bir araya getirilmesi olarak görülebilir. Böylece, daha derin aramalarla gözlemlenen performans iyileştirmesi, çok adımlı güncellemelerin kullanılmasından dolayı kaynaklanmaz. Özellikle aday eylemleriyle ilgili önemli miktarda hesaplama yaparak karar-zaman planlaması, odaklanmamış güncellemelere dayanarak üretilebilecek olandan daha iyi kararlar verebilir.

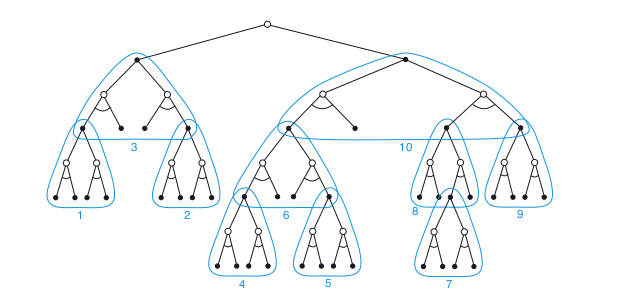
Şekil 8.9 : Sezgisel arama, yaprak düğümlerinden köke doğru değerleri yedekleyen bir adım güncellemelerinin (burada mavi olarak gösterilen) bir sırası olarak uygulanabilir. Burada gösterilen sıralama, seçici derinlik araması içindir.

Rollout Algoritmaları

Rollout algoritmaları, Monte Carlo denetimine dayanan karar-zaman planlama algoritmalarıdır. Her bir olası eylemle başlayan ve ardından verilen politikayı takip eden birçok benzetilmiş yörüngenin getirilerinin ortalaması alınarak belirli bir politikanın eylem değerlerini tahmin ederler. Aksiyon-değer tahminlerinin yeterince doğru olduğu düşünüldüğünde, en yüksek tahmini değere sahip eylem yürütülür.

Bölüm 5’te açıklanan Monte Carlo kontrol algoritmalarından farklı olarak, bir Rollout algoritmasının amacı, tam bir optimum eylem değeri fonksiyonunu tahmin etmektir. Yalnızca geçerli her bir durum için ve genel olarak yayınlama politikası olarak adlandırılan belirli bir politika için Monte Carlo tahminleri üretiyorlar. Karar-zamanı(decision-time) planlama algoritmaları olarak, Rollout algoritmaları bu eylem-değer tahminlerini derhal kullanır ve sonra bunları atar. Bu işlem Rollout durum algoritmalarının uygulanmasını basit hale getirir.

Eşitsizlik katı ise \(\pi’\) aslında \(\pi\) den daha iyidir. Bu, ‘s’ nin geçerli durum ve ‘\(\pi\)’ nin ‘rollout’ politikası olduğu rollout algoritmaları için geçerlidir. Sonuç olarak Rollout Algoritması Bölüm 4.3’te ele alınan dinamik programlamaya ilişkin politika-yineleme(policy-iteration) algoritmasının bir adımı gibidir.

Bir Rollout algoritmasının amacı, optimal bir politika bulmak değil varsayılan politikaları iyileştirmektir. Deneyimler, Rollout algoritmalarının şaşırtıcı derecede etkili olabileceğini göstermiştir. Örneğin, Tesauro ve Galperin (1997) Rollout yöntemiyle üretilen tavla oyun yeteneğindeki dramatik gelişmelere şaşırdılar. Bazı uygulamalarda, bir ‘rollout’ algoritması ‘rollout’ politikası tamamen rastgele olsa bile iyi performans sağlayabilir. İyileştirilmiş politikanın performansı, Rollout politikasının performansına ve Monte Carlo değer tahminlerinin doğruluğuna bağlıdır. Rollout politikası ve değer tahminleri ne kadar doğru olursa, Rollout algoritması tarafından üretilen politika da o kadar iyi olur.

Karar-zaman(decision-time) planlama yöntemleri olarak, rollout algoritmaları genellikle sıkı zaman kısıtlamalarını karşılamak zorundadır. Roll out algoritmasının ihtiyaç duyduğu hesaplama süresi, her bir karar için değerlendirilmesi gereken eylemlerin sayısına, faydalı örnek geri dönüşlerini elde etmek için gerekli olan simüle edilmiş yörüngelerin zaman adımlarının sayısına ve kullanıma hazır hale getirme politikasını alması gereken süreye bağlıdır.

Bu etkenlerin dengelenmesi, herhangi bir Rollout yönteminin uygulanmasında önemli olmakla birlikte, zorluğu azaltmanın birkaç yolu vardır. Monte Carlo denemeleri birbirinden bağımsız olduğu için, ayrı işlemciler üzerinde birçok denemeyi paralel olarak çalıştırmak mümkündür. Diğer bir yöntem ise simüle edilmiş yörüngelerin tam bölümlerden kısaltılmasıdır.

Rollout algoritmalarını öğrenme algoritmaları olarak düşünmüyoruz çünkü; çünkü uzun vadeli değer ya da politika hafızalarını korumazlar. Son olarak, Rollout algoritması öngörülen eylem değerlerine göre açgözlü davranarak politika geliştirme özelliğinden yararlanır.

Monte Carlo Arama Ağacı

Monte Carlo Arama Ağacı (Monte Carlo Tree Search-MCTS), yeni ve çarpıcı bir karar-zaman planlaması örneğidir. MCTS temelde bir yuvarlama(rollout) algoritmasıdır.MCTS Go bilgisayarının 2005’te amatör seviyeden 2015’te grandmaster seviyesine yükselmesinden büyük ölçüde sorumludur.Temel algoritmanın birçok varyasyonu geliştirilmiştir.MCTS, genel oyun oynama dahil olmak üzere çok çeşitli rekabet ortamlarında etkili olduğunu kanıtlamıştır, ancak bu oyunlarla sınırlı değildir. Hızlı çok adımlı simüle için yeterince basit bir ortam modeli varsa tek ajanlı sıralı karar problemleri için etkili olabilir.

MCTS, her bir yeni durumla karşılaştıktan sonra ajanın bu duruma ilişkin eylemini seçmesi için yürütülür. Bir sonraki durum için eylemi seçmek için tekrar çalıştırılır.Yuvarlama algoritmasında olduğu gibi, her yürütme, mevcut durumdan başlayarak ve bir terminal durumuna giden birçok yörüngeyi simüle eden yinelemeli bir süreçtir.MCTS’nin ana fikri, daha önceki simülasyonlardan yüksek değerlendirmeler almış olan yörüngelerin(trajectories) ilk kısımlarını genişleterek mevcut durumdan başlayarak çoklu simülasyonlara odaklanmaktır.Birçok uygulamada, bir sonraki yürütme için yararlı olması muhtemel seçilmiş eylem değerlerini koruduğu halde, MCTS, bir eylem seçiminden diğerine yaklaşık değer işlevlerini veya ilkelerini korumak zorunda değildir.

Daha ayrıntılı olarak, MCTS’nin temel bir versiyonunun her yinelemesi şekil’de gösterildiği gibi aşağıdaki dört adımdan oluşur:

Seçim: Kök düğümden başlayarak, ağacın kenarlarına eklenen eylem değerlerine dayanan bir ağaç ilkesi, bir yaprak düğümü seçmek için ağacı çaprazlar.

Genişleme: Bazı iterasyonlarda (uygulamanın detaylarına bağlı olarak) ağaç, seçilen düğümden, keşfedilmemiş eylemler yoluyla erişilen bir veya daha fazla çocuk düğümünü ekleyerek seçilen yaprak düğümünden genişletilir.

Simülasyon: Seçilen düğümden veya yeni eklenen çocuk düğümlerinden (varsa), tam bir bölümün simülasyonu, yuvarlama politikası tarafından seçilen işlemlerle yürütülür.Sonuç, ilk önce ağaç politikası ve ağacın ötesindeki yuvarlama politikası tarafından seçilen eylemlerin gerçekleştirildiği Monte Carlo testidir.

Yedekleme: Simüle edilmiş bölüm tarafından oluşturulan geri dönüş, MCTS’nin bu yinelemesinde ağaç politikası tarafından çevrilen ağacın kenarlarına eklenen eylem değerlerini güncellemek veya başlatmak için yedeklenir.Ağaçlar dışındaki yuvarlama politikası tarafından ziyaret edilen durumlar ve eylemler için hiçbir değer kaydedilmez.Şekil, simüle edilmiş yörüngenin terminal durumundan, yuvarlama politikasının başladığı ağaçtaki durum eylem düğümüne bir yedek göstererek bunu göstermektedir (Genel olarak, simüle edilmiş yörüngenin tüm geri dönüşü bu durum eylem düğümüne yedeklenir.).

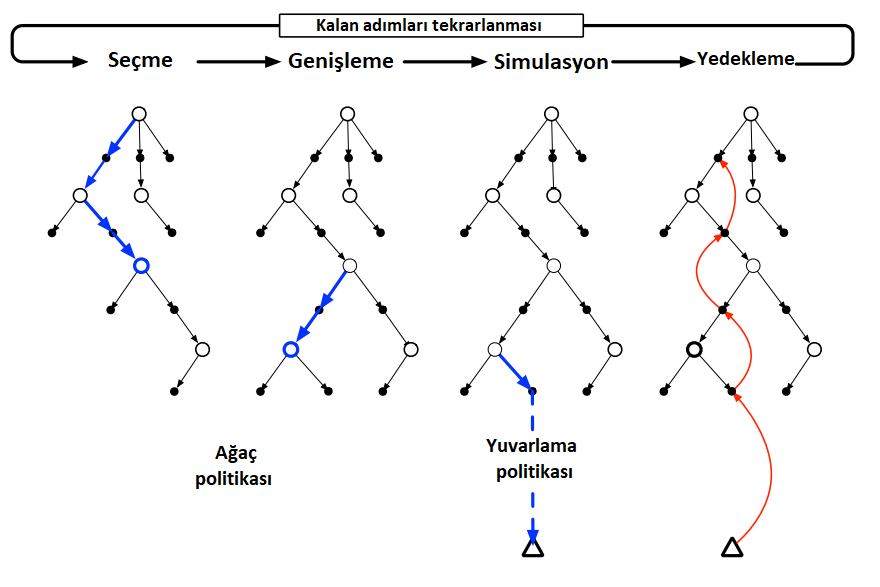
Şekil 8.10 : Monte Carlo Arama Ağacı(Monte Carlo Tree Search). Ortam yeni bir duruma dönüştüğünde,MCTS bir eylemin seçilmesi gerekmeden önce mümkün olduğunca çok yineleme gerçekleştirir ve adım adım kök düğümü mevcut durumu temsil eden bir ağaç oluşturur.

MCTS, bu dört adımı yürütmeye devam eder, her seferinde ağacın kök düğümünden, daha fazla zaman kalmayıncaya veya hesaplama kaynağı(computational source) tükenene kadar gider.Son olarak, kök düğümden (halen ortamın mevcut durumunu temsil eden) bir eylem, ağaçtaki birikmiş istatistiklere bağlı olan bazı mekanizmalara göre seçilir.Örneğin, kök durumdan erişilebilen tüm eylemlerin en büyük eylem değerine sahip olan bir eylem olabilir veya büyük olasılıkla aykırı değerleri seçmekten kaçınmak için en büyük ziyaret sayısına sahip eylem olabilir.Bu, MCTS’nin seçtiği eylemdir.Çevre yeni bir duruma geçtikten sonra, MCTS yeniden çalışır, bazen yeni durumu temsil eden tek bir kök düğümünün bir ağacıyla başlar, ancak genellikle, bir önceki tarafından yapılan ağaçtan kalan bu düğümün soyunu içeren bir ağaçla başlar.Tüm geri kalan düğümler, onlarla ilişkili eylem değerleriyle birlikte atılır.