Pekiştirmeli Öğrenme - Bölüm 10: On-policy Control With Approximation
On-policy Control With Approximation
Bu bölümde eylem-değer fonksiyonunun \(\hat{q}(s,a,\mathbf{w})\approx q_{*}(s,a)\) parametrik yaklaşımıyla kontrol problemine geri dönülmektedir.
Episodik Yarı-Gradyan Kontrolü
Ağırlık vektörü \(\mathbf{w}\) ile parametrelendirilmiş bir fonksiyonel form olarak temsil edilen, \(\hat{q}\approx q_{\pi}\) , yaklaşık eylem-değer fonksiyonudur. Daha önce \(S_{t}\mapsto U_{t}\) formundaki eğitim örnekler dikkate alınmıştı. Şimdi ise \(S_{t}, A_{t} \mapsto U_{t}\) formundaki örnekler dikkate alınmaktadır. Eylem-değer tahmini için gradyen iniş (gradient descent) güncellemesi:
\[\mathbf{w}_{t+1}\doteq \mathbf{w}_{t}+ \alpha| U_{t}-\hat{q}(S_{t},A_{t},\mathbf{w_{t}})|\nabla \hat{q}(S_{t},A_{t},\mathbf{w_{t}})\]Örneğin, tek adımlı Sarsa yöntemi için güncelleme:
\[\mathbf{w}_{t+1}\doteq \mathbf{w}_{t}+ \alpha [ R_{t+1}-\gamma\hat{q}(S_{t+1},A_{t+1},\mathbf{w_{t}})-\hat{q}(S_{t},A_{t},\mathbf{w_{t}})]\nabla \hat{q}(S_{t},A_{t},\mathbf{w_{t}})\]Bu yönteme tek-adımlı Sarsa epizodik yarı\(-\)gradyan denilmektedir. Kontrol yöntemlerini oluşturmak için, bu tür eylem\(-\)değer tahmin yöntemlerini politika geliştirme ve eylem seçimi teknikleriyle birleştirmek gerekmektedir.
Örnek 10.1 : Mountain Car Görevi
Aşağıdaki diyagramda gösterildiği gibi güçlü bir dağ yolunda güçlü bir bir arabayı kullanma görevi düşünülürse zorluk, yer çekiminin otomobilin motorundan güçlü olması ve dik yokuşta bile hızlanamamasıdır.
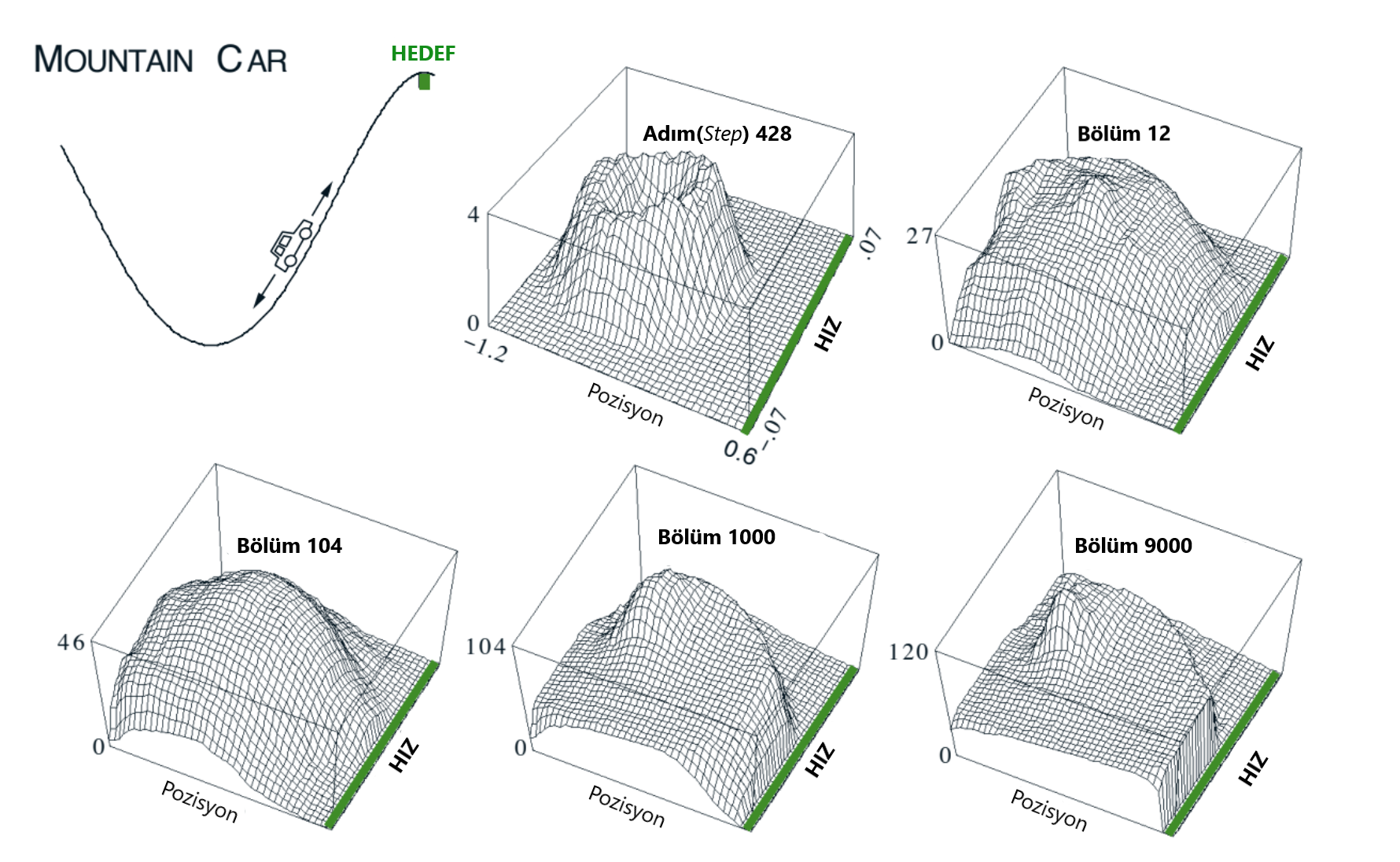
Şekil 10.1 : The Mountain Car Görevi (sol üst panel) tek seferde öğrenilen ilerleme maliyetin fonksiyonu :\((- max_{a} \hat{q}(s,a,w))\)
Tek çözüm ilk olarak hedeften uzaklaşmak ve sol taraftaki zıt eğimi ortadan kaldırmaktır. Daha sonra, araç tam gazla yol boyunca yavaşlasa bile yokuş yukarı çıkmak için yeterli durgunluğa (interia) sahip olmaktadır.
Dağın zirvesinde arabanın taşıdığı hedef pozisyona kadar bütün süredeki adımlar üzerindeki ödül bu problemde \(-1'\)dir. \(3\) tane eylem vardır: tam gaz ileri\((+1)\), tam gaz geri\((-1)\) ve sıfır gaz\((0)\). Arabanın pozisyonu \(x_t\), hızı \(\dot{x}_t\) ve güncellemesi:
\[x_{t+1} \dot{=} bound\big[x_t+\dot{x}_{t+1}\big]\] \[\dot{x}_{t+1} \dot{=} bound\big[\dot{x}_t + 0.001 A_t - 0.0025cos(3x_t)\big]\]Kısıtlama işlemi \(-1.2 \le x_{t+1} \le 0.5\) ve \(-0.07 \le \dot{x}_{t+1} \le 0.07\) olarak uygulanmaktadır. Kare kodlama yöntemiyle oluşturulan özellik vektörleri \((x(s,a))\) eylem\(-\)değer fonksiyonlarına yaklaşmak için parametre vektörleriyle doğrusal olarak birleştirilmiştir:
\[\hat{q}(s,a,w) \dot{=} w^T x(s,a) = \displaystyle\sum\limits_{i=1}^d w_i \cdot x_i(s,a)\]N-adımlı Yarı-Gradyen Sarsa
Yarı\(-\)gradyen Sarsa güncelleme eşitliğinde hedef güncelleme olarak \(n-\)adımlı getiri kullanılarak epizodik yarı\(-\)gradyen Sarsa’nın \(n-\)adımlı versiyonu elde edilmektedir. \(n-\)adımlı getiriden fonksiyon yaklaşımına aşağıdaki gibi bir genelleştirme yapılmaktadır.
\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n \hat{q} (S_{t+n}, A_{t+n}, w_{t+n-1}), t+n < T,\]
Eğer \(n+t >= T\) olursa \(G_{t:t+1} = G_t\) olmaktadır. Buradan \(n-\)adımlı ağırlık güncellemesi ise:
\[w_{t+n} \doteq w_{t+n-1} + a \big[G_{t:t+n} - \hat{q} (S_t, A_t, w_{t+n-1})\big] \triangledown \hat{q}(S_t, A_t, w_{t+n-1}),\]
olarak ifade edilmektedir. Aşağıda epizodik \(n-\)adımlı yarı\(-\)gradyen Sarsa’nın kaba kodu verilmiştir.

Ortalama Ödül: Devam Eden Görevler İçin Yeni Bir Problem Düzenlemesi
Ortalama ödül düzenlemesi, ajan ve çevre arasındaki etkileşimin sona ermeden veya başlama durumları olmadan devam ettiği problemlerdir.
Ortalama ödül düzenlemesinde, politika \(\pi'\)nin kalitesi ödül oranının ortalaması gibi veya politika takip edildiğinde \(r(\pi)\), aşağıdaki gibi tanımlanabilir:
\[r(\pi) \doteq \lim_{h \rightarrow \infty} \dfrac{1}{h} \displaystyle \sum\limits_{t = 1}^h E[R_t \mid S_0, A_{0:t-1} \sim \pi]\] \[= \lim_{t \rightarrow \infty} E [R_t \mid S_0, A_{0:t-1} \sim \pi],\] \[= \displaystyle \sum\limits_{s} \mu_\pi (s) \displaystyle \sum\limits_{a} \pi(a \mid s) \displaystyle \sum\limits_{a^1,r} p(s', r \mid s, a)r,\]MDP hakkındaki bu varsayım ergodiklik (ergodicity) olarak bilinmektedir. Bu, MDP’nin başladığı veya bir ajan tarafından verilen erken kararın geçici bir etkiye sahip olabileceği anlamına gelmektedir. Ergodiklik, yukarıdaki denklemlerdeki sınırların varlığını garanti etmek için yeterlidir. Sabit durum dağılımı, \(\pi'\)ye göre eylemler seçilirse aşağıdaki gibi aynı dağıtımda kalan özel bir dağıtım haline gelmektedir:
\[\displaystyle \sum\limits_{s} \mu_\pi (s) \displaystyle \sum\limits_{a} \pi(a \mid s) p (s' \mid s,a) = \mu_\pi(s')\]Ortalama ödül düzenlemesinde getiriler, ödüller ve ortalama ödül arasındaki farklarla tanımlanmaktadır ve diferansiyel getiri olarak bilinmektedir. Karşılık gelen değer fonksiyonları ise diferansiyel değer fonksiyonları olarak bilinmektedir.
\[G_t \doteq R_{t+1} - r(\pi) + R_{t+2} - r(\pi) + R_{t+3} - r(\pi) + \cdots\]Diferansiyel değer fonksiyonları, Bellman denklemleriyle benzer yapıdadır. Tüm \(\gamma'\)lar çıkarılmaktadır. Tüm ödüller ise, ödül ve gerçek ortalama ödül arasındaki farkla değiştirilmektedir.
\(v_\pi (s) = \displaystyle \sum\limits_a (a \mid s) \displaystyle \sum\limits_{r,s^1} p(s', r \mid s,a) \big[r - r(\pi) + v_\pi (s') \big],\) \(q_\pi(s,a) = \displaystyle \sum\limits_{r,s'} p(s',r \mid s,a) \big[ r - r(\pi) + \displaystyle \sum\limits_{a'} \pi(a' \mid s') q_\pi (s',a')\big]\) \(v_{*}(s) = \max\limits_a \displaystyle \sum\limits_{r,s'} p(s',r \mid s,a) \big[r - \max\limits_\pi r(\pi) + v_*(s') \big], and\) \(q_{*}(s,a) = \displaystyle \sum\limits_{r,s'} p(s',r \mid s,a) \big[r - \max\limits_\pi r(\pi) + \max\limits_{a'} q_{*} (s',a')\big]\)
İndirgenmiş Düzenlemenin Kullanımdan Kaldırılması
Devam eden problemlerin formülasyonu, her durum getirilerinin ayrı ayrı tanımlanabildiği ve ortalaması alınabileceği tablo halinde çok faydalı olmuştur. Ancak eş zamanlı olaylarda, bu problem formülasyonunu kullanmanın gerekip gerekmediği tartışılmaktadır.
Nedenini görmek için, herhangi bir başlangıç veya son olmaksızın sonsuz sayıda getiri düşünüldüğünde açıkça tanımlanan durumlar bulunmamaktadır. Durumlar, yalnızca durumları birbirinden ayırmak için çok az şey yapan özellik vektörleri tarafından temsil edilmektedir.
Aslında politika için indirgenmiş getirilerin ortalaması her zaman \(r(\pi) = \frac{1}{1-\gamma}\) yani gerçek ortalama ödül \(r(\pi)'\)dir. Bu nedenle indirgenme oranı gamanın problem formülasyonu üzerinde etkisi yoktur.
İndirgenmiş olarak her ödül, getiri olduğunda her pozisyonda bir kez görünmektedir. \(t.\) ödülü, bir getiride indirgemeyip \(1\) getiri \(2.\) getiride indirgenip, \(t - 1000.\) getiride \(999\) kez indirgenme olmaktadır. Bu ödülün ağırlığı: \(1+\gamma+\gamma^2 + \cdots = \dfrac{1}{1-\gamma}\) olmaktadır. Bütün durumlar için aynı olduğu için, hepsi aynı şekilde indirgenmekte ve getirilerin ortalaması, bu kez ortalama ödül veya \(\frac{r(\pi)}{1-\gamma}\) olmaktadır.
Sonuç olarak indirgenme parametresi \(\gamma\), bir problem parametresinden çözüm metotu parametresine dönüşmektedir.
Diferansiyel Yarı-Gradyende \(n-\)adımlı Sarsa
\(n\)\(-\)adımlı paketlemeyi genelleştirmek için zamansal fark hatasının \(n\)\(-\)adımlı bir versiyonuna ihtiyaç vardır. \(n-\)adımlı getiriyi diferansiyel formuna, fonksiyon yaklaşımıyla genelleştirerek başlanır:
\[G_{t:t+n} \dot{=} R_{t+1} - \bar{R}_{t+1} + R_{t+2} - \bar{R}_{t+2} + ... + + R_{t+n} - \bar{R}_{t+n} + \hat{q}(S_{t+n}, A_{t+n}, w_{t+n-1})\]Daha sonra zamansal fark hatası:
\(\delta \doteq G_{t:t+n} - \hat{q}(S_t, A_t, w)\) olarak bulunur. Sözde kod için aşağıda algoritma verilmiştir.

\(\hat{q} : S x A x \mathbb{R}^d \rightarrow \mathbb{R}\) a policy \(\pi\) \(\mathcal{w} \in \mathbb{R}^d\) arbitrarily \((w=0)\)
